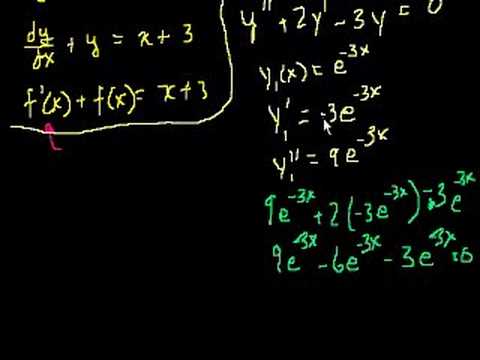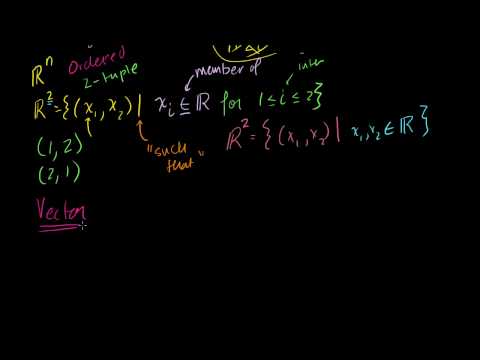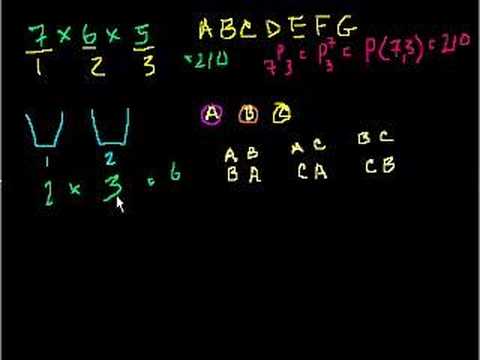Online courses directory (418)

Calculus One is a first introduction to differential and integral calculus, emphasizing engaging examples from everyday life.

Divergence theorem intuition. Divergence theorem examples and proofs. Types of regions in 3D. 3-D Divergence Theorem Intuition. Divergence Theorem Example 1. Why we got zero flux in Divergence Theorem Example 1. Type I Regions in Three Dimensions. Type II Regions in Three Dimensions. Type III Regions in Three Dimensions. Divergence Theorem Proof (part 1). Divergence Theorem Proof (part 2). Divergence Theorem Proof (part 3). Divergence Theorem Proof (part 4). Divergence Theorem Proof (part 5). 3-D Divergence Theorem Intuition. Divergence Theorem Example 1. Why we got zero flux in Divergence Theorem Example 1. Type I Regions in Three Dimensions. Type II Regions in Three Dimensions. Type III Regions in Three Dimensions. Divergence Theorem Proof (part 1). Divergence Theorem Proof (part 2). Divergence Theorem Proof (part 3). Divergence Theorem Proof (part 4). Divergence Theorem Proof (part 5).

Limit introduction, squeeze theorem, and epsilon-delta definition of limits. Introduction to limits. Limit at a point of discontinuity. Determining which limit statements are true. Limit properties. Limit example 1. Limits 1. One-sided limits from graphs. One-sided limits from graphs. Introduction to Limits. Limit Examples (part 1). Limit Examples (part 2). Limit Examples (part 3). Limit Examples w/ brain malfunction on first prob (part 4). More Limits. Limits 1. Limits and infinity. Limits at positive and negative infinity. More limits at infinity. Limits with two horizontal asymptotes. Limits 2. Squeeze Theorem. Proof: lim (sin x)/x. Limit intuition review. Building the idea of epsilon-delta definition. Epsilon-delta definition of limits. Proving a limit using epsilon-delta definition. Limits to define continuity. Continuity. Epsilon Delta Limit Definition 1. Epsilon Delta Limit Definition 2. Introduction to limits. Limit at a point of discontinuity. Determining which limit statements are true. Limit properties. Limit example 1. Limits 1. One-sided limits from graphs. One-sided limits from graphs. Introduction to Limits. Limit Examples (part 1). Limit Examples (part 2). Limit Examples (part 3). Limit Examples w/ brain malfunction on first prob (part 4). More Limits. Limits 1. Limits and infinity. Limits at positive and negative infinity. More limits at infinity. Limits with two horizontal asymptotes. Limits 2. Squeeze Theorem. Proof: lim (sin x)/x. Limit intuition review. Building the idea of epsilon-delta definition. Epsilon-delta definition of limits. Proving a limit using epsilon-delta definition. Limits to define continuity. Continuity. Epsilon Delta Limit Definition 1. Epsilon Delta Limit Definition 2.

Line integral of scalar and vector-valued functions. Green's theorem and 2-D divergence theorem. Introduction to the Line Integral. Line Integral Example 1. Line Integral Example 2 (part 1). Line Integral Example 2 (part 2). Position Vector Valued Functions. Derivative of a position vector valued function. Differential of a vector valued function. Vector valued function derivative example. Line Integrals and Vector Fields. Using a line integral to find the work done by a vector field example. Parametrization of a Reverse Path. Scalar Field Line Integral Independent of Path Direction. Vector Field Line Integrals Dependent on Path Direction. Path Independence for Line Integrals. Closed Curve Line Integrals of Conservative Vector Fields. Example of Closed Line Integral of Conservative Field. Second Example of Line Integral of Conservative Vector Field. Green's Theorem Proof Part 1. Green's Theorem Proof (part 2). Green's Theorem Example 1. Green's Theorem Example 2. Constructing a unit normal vector to a curve. 2 D Divergence Theorem. Conceptual clarification for 2-D Divergence Theorem. Introduction to the Line Integral. Line Integral Example 1. Line Integral Example 2 (part 1). Line Integral Example 2 (part 2). Position Vector Valued Functions. Derivative of a position vector valued function. Differential of a vector valued function. Vector valued function derivative example. Line Integrals and Vector Fields. Using a line integral to find the work done by a vector field example. Parametrization of a Reverse Path. Scalar Field Line Integral Independent of Path Direction. Vector Field Line Integrals Dependent on Path Direction. Path Independence for Line Integrals. Closed Curve Line Integrals of Conservative Vector Fields. Example of Closed Line Integral of Conservative Field. Second Example of Line Integral of Conservative Vector Field. Green's Theorem Proof Part 1. Green's Theorem Proof (part 2). Green's Theorem Example 1. Green's Theorem Example 2. Constructing a unit normal vector to a curve. 2 D Divergence Theorem. Conceptual clarification for 2-D Divergence Theorem.

Thinking about forms of derivatives in multi-dimensions and for vector-valued functions: partial derivatives, gradient, divergence and curl. Partial Derivatives. Partial Derivatives 2. Gradient 1. Gradient of a scalar field. Divergence 1. Divergence 2. Divergence 3. Curl 1. Curl 2. Curl 3. Partial Derivatives. Partial Derivatives 2. Gradient 1. Gradient of a scalar field. Divergence 1. Divergence 2. Divergence 3. Curl 1. Curl 2. Curl 3.

Sequences, series and approximating functions. Maclaurin and Taylor series. Sequences and Series (part 1). Sequences and series (part 2). Maclaurin and Taylor Series Intuition. Cosine Taylor Series at 0 (Maclaurin). Sine Taylor Series at 0 (Maclaurin). Taylor Series at 0 (Maclaurin) for e to the x. Euler's Formula and Euler's Identity. Visualizing Taylor Series Approximations. Generalized Taylor Series Approximation. Visualizing Taylor Series for e^x. Error or Remainder of a Taylor Polynomial Approximation. Proof: Bounding the Error or Remainder of a Taylor Polynomial Approximation. Polynomial approximation of functions (part 1). Polynomial approximation of functions (part 2). Approximating functions with polynomials (part 3). Polynomial approximation of functions (part 4). Polynomial approximations of functions (part 5). Polynomial approximation of functions (part 6). Polynomial approximation of functions (part 7). Taylor Polynomials. Sequences and Series (part 1). Sequences and series (part 2). Maclaurin and Taylor Series Intuition. Cosine Taylor Series at 0 (Maclaurin). Sine Taylor Series at 0 (Maclaurin). Taylor Series at 0 (Maclaurin) for e to the x. Euler's Formula and Euler's Identity. Visualizing Taylor Series Approximations. Generalized Taylor Series Approximation. Visualizing Taylor Series for e^x. Error or Remainder of a Taylor Polynomial Approximation. Proof: Bounding the Error or Remainder of a Taylor Polynomial Approximation. Polynomial approximation of functions (part 1). Polynomial approximation of functions (part 2). Approximating functions with polynomials (part 3). Polynomial approximation of functions (part 4). Polynomial approximations of functions (part 5). Polynomial approximation of functions (part 6). Polynomial approximation of functions (part 7). Taylor Polynomials.

Using definite integrals with the shell and disc methods to find volumes of solids of revolution. Disk method around x-axis. Generalizing disc method around x-axis. Disc method around y-axis. Disc method (washer method) for rotation around x-axis. Generalizing the washer method. Disc method rotation around horizontal line. Washer method rotating around non-axis. Part 2 of washer for non axis rotation. Disc method rotating around vertical line. Calculating integral disc method around vertical line. Washer or ring method for vertical line rotation. Evaluating integral for washer method around vertical line. Shell method for rotating around vertical line. Evaluating integral for shell method example. Shell method for rotating around horizontal line. Shell method with two functions of x. Calculating integral with shell method. Shell method with two functions of y. Part 2 of shell method with 2 functions of y. Disc method: function rotated about x-axis. Disc method (rotating f(x) about x axis). Volume of a sphere. Disc method with outer and inner function boundaries. Shell method to rotate around y-axis. Disk method: rotating x=f(y) around the y-axis. Shell method around a non-axis line. Shell method around a non-axis line 2. Disk method around x-axis. Generalizing disc method around x-axis. Disc method around y-axis. Disc method (washer method) for rotation around x-axis. Generalizing the washer method. Disc method rotation around horizontal line. Washer method rotating around non-axis. Part 2 of washer for non axis rotation. Disc method rotating around vertical line. Calculating integral disc method around vertical line. Washer or ring method for vertical line rotation. Evaluating integral for washer method around vertical line. Shell method for rotating around vertical line. Evaluating integral for shell method example. Shell method for rotating around horizontal line. Shell method with two functions of x. Calculating integral with shell method. Shell method with two functions of y. Part 2 of shell method with 2 functions of y. Disc method: function rotated about x-axis. Disc method (rotating f(x) about x axis). Volume of a sphere. Disc method with outer and inner function boundaries. Shell method to rotate around y-axis. Disk method: rotating x=f(y) around the y-axis. Shell method around a non-axis line. Shell method around a non-axis line 2.

Differential equations with only first derivatives. What is a differential equation. Simple Differential Equations. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2. What is a differential equation. Simple Differential Equations. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2.

Transforms and the Laplace transform in particular. Convolution integrals. Laplace Transform 1. Laplace Transform 2. L{sin(at)}) - transform of sin(at). Part 2 of the transform of the sin(at). Laplace as linear operator and Laplace of derivatives. Laplace Transform of cos t and polynomials. "Shifting" transform by multiplying function by exponential. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace/Step Function Differential Equation. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob. Laplace Transform 1. Laplace Transform 2. L{sin(at)}) - transform of sin(at). Part 2 of the transform of the sin(at). Laplace as linear operator and Laplace of derivatives. Laplace Transform of cos t and polynomials. "Shifting" transform by multiplying function by exponential. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace/Step Function Differential Equation. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob.

Linear differential equations that contain second derivatives. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4.

We explore creating and moving between various coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems.

Let's get our feet wet by thinking in terms of vectors and spaces. Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A).

Understanding how we can map one set of vectors to another set. Matrices used to define linear transformations. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible.

2003 AIME II Problem 1. 2003 AIME II Problem 3. Sum of factors of 27000. Sum of factors 2. 2003 AIME II Problem 4 (part 1). 2003 AIME II Problem 4 (part 2). 2003 AIME II Problem 5. 2003 AIME II Problem 5 Minor Correction. Area Circumradius Formula Proof. 2003 AIME II Problem 6. 2003 AIME II Problem 7. 2003 AIME II Problem 8. Sum of Polynomial Roots (Proof). Sum of Squares of Polynomial Roots. 2003 AIME II Problem 9. 2003 AIME II Problem 10. 2003 AIME II Problem 11. 2003 AIME II Problem 12. 2003 AIME II Problem 13. 2003 AIME II Problem 14. 2003 AIME II Problem 15 (part 1). 2003 AIME II Problem 15 (part 2). 2003 AIME II Problem 15 (part 3). 2003 AIME II Problem 1. 2003 AIME II Problem 3. Sum of factors of 27000. Sum of factors 2. 2003 AIME II Problem 4 (part 1). 2003 AIME II Problem 4 (part 2). 2003 AIME II Problem 5. 2003 AIME II Problem 5 Minor Correction. Area Circumradius Formula Proof. 2003 AIME II Problem 6. 2003 AIME II Problem 7. 2003 AIME II Problem 8. Sum of Polynomial Roots (Proof). Sum of Squares of Polynomial Roots. 2003 AIME II Problem 9. 2003 AIME II Problem 10. 2003 AIME II Problem 11. 2003 AIME II Problem 12. 2003 AIME II Problem 13. 2003 AIME II Problem 14. 2003 AIME II Problem 15 (part 1). 2003 AIME II Problem 15 (part 2). 2003 AIME II Problem 15 (part 3).

The AMC 10 is part of the series of contests administered by the MAA American Mathematics Competitions that determines the United States team in the International Math Olympiad. The AMC 10 is a 25 question, 75 minute multiple choice test for students in 10th grade or below. Two versions of the AMC 10 are offered each year. 2013 AMC 10 A #21 / AMC 12 A #17. 2013 AMC 10 A #22 / AMC 12 A #18. 2013 AMC 10 A #23 / AMC 12 A #19. 2013 AMC 10 A #24. 2013 AMC 10 A #25. 2013 AMC 10 A #21 / AMC 12 A #17. 2013 AMC 10 A #22 / AMC 12 A #18. 2013 AMC 10 A #23 / AMC 12 A #19. 2013 AMC 10 A #24. 2013 AMC 10 A #25.

This tutorial is the meat of much of classical physics. We think about what a force is and how Newton changed the world's (and possibly your) view of how reality works. Newton's First Law of Motion. Newton's First Law of Motion Concepts. Newton's First Law of Motion. Newton's First Law. Newton's Second Law of Motion. Newton's Third Law of Motion. Newton's Third Law of Motion. All of Newton's Laws of Motion. Normal Force and Contact Force. Normal Force in an Elevator. Balanced and Unbalanced Forces. Unbalanced Forces and Motion. Slow Sock on Lubricon VI. Normal Forces on Lubricon VI. Inclined Plane Force Components. Ice Accelerating Down an Incline. Force of Friction Keeping the Block Stationary. Correction to Force of Friction Keeping the Block Stationary. Force of Friction Keeping Velocity Constant. Intuition on Static and Kinetic Friction Comparisons. Static and Kinetic Friction Example. Introduction to Tension. Introduction to Tension (Part 2). Tension in an accelerating system and pie in the face. Newton's First Law of Motion. Newton's First Law of Motion Concepts. Newton's First Law of Motion. Newton's First Law. Newton's Second Law of Motion. Newton's Third Law of Motion. Newton's Third Law of Motion. All of Newton's Laws of Motion. Normal Force and Contact Force. Normal Force in an Elevator. Balanced and Unbalanced Forces. Unbalanced Forces and Motion. Slow Sock on Lubricon VI. Normal Forces on Lubricon VI. Inclined Plane Force Components. Ice Accelerating Down an Incline. Force of Friction Keeping the Block Stationary. Correction to Force of Friction Keeping the Block Stationary. Force of Friction Keeping Velocity Constant. Intuition on Static and Kinetic Friction Comparisons. Static and Kinetic Friction Example. Introduction to Tension. Introduction to Tension (Part 2). Tension in an accelerating system and pie in the face.

Measures of central tendency and dispersion. Mean, median, mode, variance, and standard deviation. Statistics intro: mean, median and mode. Example: Finding mean, median and mode. Mean median and mode. Exploring Mean and Median Module. Exploring mean and median. Average word problems. Sample mean versus population mean.. Reading Box-and-Whisker Plots. Constructing a box-and-whisker plot. Box-and-Whisker Plots. Creating box and whisker plots. Example: Range and mid-range. Range, Variance and Standard Deviation as Measures of Dispersion. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Unbiased Estimate of Population Variance. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Will it converge towards -1?. Variance. Population standard deviation. Sample standard deviation and bias. Statistics: Standard Deviation. Exploring Standard Deviation 1 Module. Exploring standard deviation 1. Standard deviation. Statistics: Alternate Variance Formulas. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance. Statistics intro: mean, median and mode. Example: Finding mean, median and mode. Mean median and mode. Exploring Mean and Median Module. Exploring mean and median. Average word problems. Sample mean versus population mean.. Reading Box-and-Whisker Plots. Constructing a box-and-whisker plot. Box-and-Whisker Plots. Creating box and whisker plots. Example: Range and mid-range. Range, Variance and Standard Deviation as Measures of Dispersion. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Unbiased Estimate of Population Variance. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Will it converge towards -1?. Variance. Population standard deviation. Sample standard deviation and bias. Statistics: Standard Deviation. Exploring Standard Deviation 1 Module. Exploring standard deviation 1. Standard deviation. Statistics: Alternate Variance Formulas. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance.

Introduction to probability. Independent and dependent events. Compound events. Mutual exclusive events. Addition rule for probability. Basic Probability. Probability space exercise example. Probability space. Example: Marbles from a bag. Example: Picking a non-blue marble. Example: Picking a yellow marble. Probability 1. Probability with Playing Cards and Venn Diagrams. Addition Rule for Probability. Compound Probability of Independent Events. Getting At Least One Heads. Example: Probability of rolling doubles. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Frequency Probability and Unfair Coins. Example: Getting two questions right on an exam. Example: Rolling even three times. Independent probability. Frequency Stability. Introduction to dependent probability. Example: Dependent probability. Example: Is an event independent or dependent?. Example: Bag of unfair coins. Dependent probability. Monty Hall Problem. Intersection and union of sets. Relative complement or difference between sets. Universal set and absolute complement. Subset, strict subset, and superset. Bringing the set operations together. Basic set notation. Probability (part 1). Probability (part 2). Probability (part 3). Probability (part 4). Probability (part 5). Probability (part 6). Probability (part 7). Probability (part 8). Introduction to Random Variables. Basic Probability. Probability space exercise example. Probability space. Example: Marbles from a bag. Example: Picking a non-blue marble. Example: Picking a yellow marble. Probability 1. Probability with Playing Cards and Venn Diagrams. Addition Rule for Probability. Compound Probability of Independent Events. Getting At Least One Heads. Example: Probability of rolling doubles. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Frequency Probability and Unfair Coins. Example: Getting two questions right on an exam. Example: Rolling even three times. Independent probability. Frequency Stability. Introduction to dependent probability. Example: Dependent probability. Example: Is an event independent or dependent?. Example: Bag of unfair coins. Dependent probability. Monty Hall Problem. Intersection and union of sets. Relative complement or difference between sets. Universal set and absolute complement. Subset, strict subset, and superset. Bringing the set operations together. Basic set notation. Probability (part 1). Probability (part 2). Probability (part 3). Probability (part 4). Probability (part 5). Probability (part 6). Probability (part 7). Probability (part 8). Introduction to Random Variables.

Permutations and combinations. Using combinatorics to solve questions in probability. Permutations. Combinations. Counting 2. Example: Ways to arrange colors. Example: 9 card hands. Example: Ways to pick officers. Permutations. Combinations. Permutations and combinations. Example: Probability through counting outcomes. Example: All the ways you can flip a coin. Getting Exactly Two Heads (Combinatorics). Probability and Combinations (part 2). Probability using Combinations. Exactly Three Heads in Five Flips. Example: Different ways to pick officers. Example: Combinatorics and probability. Example: Lottery probability. Mega Millions Jackpot Probability. Generalizing with Binomial Coefficients (bit advanced). Conditional Probability and Combinations. Conditional Probability (Bayes Theorem) Visualized. Birthday Probability Problem. Probability with permutations and combinations. Permutations. Combinations. Counting 2. Example: Ways to arrange colors. Example: 9 card hands. Example: Ways to pick officers. Permutations. Combinations. Permutations and combinations. Example: Probability through counting outcomes. Example: All the ways you can flip a coin. Getting Exactly Two Heads (Combinatorics). Probability and Combinations (part 2). Probability using Combinations. Exactly Three Heads in Five Flips. Example: Different ways to pick officers. Example: Combinatorics and probability. Example: Lottery probability. Mega Millions Jackpot Probability. Generalizing with Binomial Coefficients (bit advanced). Conditional Probability and Combinations. Conditional Probability (Bayes Theorem) Visualized. Birthday Probability Problem. Probability with permutations and combinations.

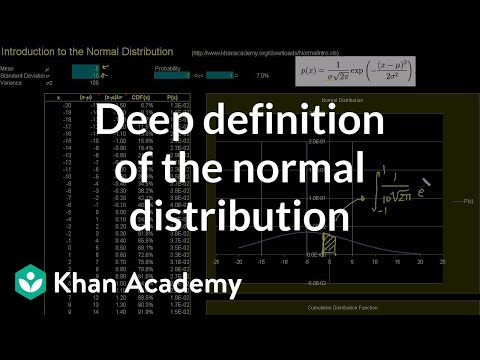
Making inferences based on sample data. Confidence intervals. Margin of error. Hypothesis testing. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. Empirical rule. ck12.org: More Empirical Rule and Z-score practice. Z scores 1. Z scores 2. Z scores 3. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Small Sample Size Confidence Intervals. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Type 1 Errors. Z-statistics vs. T-statistics. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. Empirical rule. ck12.org: More Empirical Rule and Z-score practice. Z scores 1. Z scores 2. Z scores 3. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Small Sample Size Confidence Intervals. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Type 1 Errors. Z-statistics vs. T-statistics. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic.