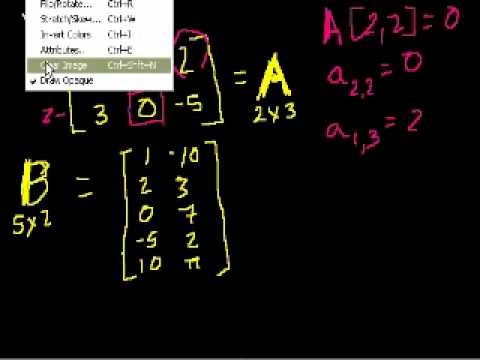
Online courses directory (418)

The course consists of a sampling of topics from algebraic combinatorics. The topics include the matrix-tree theorem and other applications of linear algebra, applications of commutative and exterior algebra to counting faces of simplicial complexes, and applications of algebra to tilings.

The main aims of this seminar will be to go over the classification of surfaces (Enriques-Castelnuovo for characteristic zero, Bombieri-Mumford for characteristic p), while working out plenty of examples, and treating their geometry and arithmetic as far as possible.

This course provides an introduction to algebraic number theory. Topics covered include dedekind domains, unique factorization of prime ideals, number fields, splitting of primes, class group, lattice methods, finiteness of the class number, Dirichlet's units theorem, local fields, ramification, discriminants.

Questions from previous IIT JEEs. IIT JEE Trigonometry Problem 1. IIT JEE Perpendicular Planes (Part 1). IIT JEE Perpendicular Plane (part 2). IIT JEE Complex Root Probability (part 1). IIT JEE Complex Root Probability (part 2). IIT JEE Position Vectors. IIT JEE Integral Limit. IIT JEE Algebraic Manipulation. IIT JEE Function Maxima. IIT JEE Diameter Slope. IIT JEE Hairy Trig and Algebra (part 1). IIT JEE Hairy Trig and Algebra (Part 2). IIT JEE Hairy Trig and Algebra (Part 3). IIT JEE Complex Numbers (part 1). IIT JEE Complex Numbers (part 2). IIT JEE Complex Numbers (part 3). IIT JEE Differentiability and Boundedness. IIT JEE Integral with Binomial Expansion. IIT JEE Symmetric and Skew-Symmetric Matrices. IIT JEE Trace and Determinant. IIT JEE Divisible Determinants. IIT JEE Circle Hyperbola Intersection. IIT JEE Circle Hyperbola Common Tangent Part 1. IIT JEE Circle Hyperbola Common Tangent Part 2. IIT JEE Circle Hyperbola Common Tangent Part 3. IIT JEE Circle Hyperbola Common Tangent Part 4. IIT JEE Circle Hyperbola Common Tangent Part 5. IIT JEE Trigonometric Constraints. IIT JEE Trigonometric Maximum. Vector Triple Product Expansion (very optional). IIT JEE Lagrange's Formula. Tangent Line Hyperbola Relationship (very optional). 2010 IIT JEE Paper 1 Problem 50 Hyperbola Eccentricity. Normal vector from plane equation. Point distance to plane. Distance Between Planes. Complex Determinant Example. Series Sum Example. Trigonometric System Example. Simple Differential Equation Example. IIT JEE Trigonometry Problem 1. IIT JEE Perpendicular Planes (Part 1). IIT JEE Perpendicular Plane (part 2). IIT JEE Complex Root Probability (part 1). IIT JEE Complex Root Probability (part 2). IIT JEE Position Vectors. IIT JEE Integral Limit. IIT JEE Algebraic Manipulation. IIT JEE Function Maxima. IIT JEE Diameter Slope. IIT JEE Hairy Trig and Algebra (part 1). IIT JEE Hairy Trig and Algebra (Part 2). IIT JEE Hairy Trig and Algebra (Part 3). IIT JEE Complex Numbers (part 1). IIT JEE Complex Numbers (part 2). IIT JEE Complex Numbers (part 3). IIT JEE Differentiability and Boundedness. IIT JEE Integral with Binomial Expansion. IIT JEE Symmetric and Skew-Symmetric Matrices. IIT JEE Trace and Determinant. IIT JEE Divisible Determinants. IIT JEE Circle Hyperbola Intersection. IIT JEE Circle Hyperbola Common Tangent Part 1. IIT JEE Circle Hyperbola Common Tangent Part 2. IIT JEE Circle Hyperbola Common Tangent Part 3. IIT JEE Circle Hyperbola Common Tangent Part 4. IIT JEE Circle Hyperbola Common Tangent Part 5. IIT JEE Trigonometric Constraints. IIT JEE Trigonometric Maximum. Vector Triple Product Expansion (very optional). IIT JEE Lagrange's Formula. Tangent Line Hyperbola Relationship (very optional). 2010 IIT JEE Paper 1 Problem 50 Hyperbola Eccentricity. Normal vector from plane equation. Point distance to plane. Distance Between Planes. Complex Determinant Example. Series Sum Example. Trigonometric System Example. Simple Differential Equation Example.

Basic probability. Should have a reasonable grounding in basic algebra before watching. Basic Probability. Example: Marbles from a bag. Example: Picking a non-blue marble. Example: Picking a yellow marble. Term Life Insurance and Death Probability. Probability with Playing Cards and Venn Diagrams. Addition Rule for Probability. Compound Probability of Independent Events. Getting At Least One Heads. Example: Probability of rolling doubles. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Frequency Probability and Unfair Coins. Example: Getting two questions right on an exam. Example: Rolling even three times. Introduction to dependent probability. Example: Dependent probability. Example: Is an event independent or dependent?. Example: Bag of unfair coins. Monty Hall Problem. Example: All the ways you can flip a coin. Example: Probability through counting outcomes. Permutations. Combinations. Example: Ways to arrange colors. Example: 9 card hands. Example: Ways to pick officers. Getting Exactly Two Heads (Combinatorics). Probability and Combinations (part 2). Probability using Combinations. Exactly Three Heads in Five Flips. Generalizing with Binomial Coefficients (bit advanced). Example: Different ways to pick officers. Example: Combinatorics and probability. Example: Lottery probability. Mega Millions Jackpot Probability. Conditional Probability and Combinations. Birthday Probability Problem. Random Variables. Discrete and continuous random variables. Probability Density Functions. Expected Value: E(X). Binomial Distribution 1. Binomial Distribution 2. Binomial Distribution 3. Binomial Distribution 4. Expected Value of Binomial Distribution. Poisson Process 1. Poisson Process 2. Law of Large Numbers. Introduction to Random Variables. Probability (part 1). Probability (part 2). Probability (part 3). Probability (part 4). Probability (part 5). Probability (part 6). Probability (part 7). Probability (part 8).

The goal of this course is to describe some of the tools which enter into the proof of Sullivan's conjecture.

Finding measurements and applying and proving circle theorems. Language and Notation of the Circle. Circles: Radius, Diameter and Circumference. Parts of a Circle. Three Points Defining a Circle. Area of a Circle. Pi Is (still) Wrong.. Right Triangles Inscribed in Circles (Proof). Right Triangles Inscribed in Circles (Proof). Perpendicular Radius Bisects Chord. Incenter and incircles of a triangle. Inradius Perimeter and Area.

Understanding the purpose, notation, and building blocks of geometry. Euclid as the Father of Geometry. Language and Notation of Basic Geometry. Lines, Line Segments, and Rays. Identifying Rays. Identifying Parallel and Perpendicular Lines.

Matrices, vectors, vector spaces, transformations. Covers all topics in a first year college linear algebra course. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra. Introduction to matrices. Matrix multiplication (part 1). Matrix multiplication (part 2). Idea Behind Inverting a 2x2 Matrix. Inverting matrices (part 2). Inverting Matrices (part 3). Matrices to solve a system of equations. Matrices to solve a vector combination problem. Singular Matrices. 3-variable linear equations (part 1). Solving 3 Equations with 3 Unknowns. Introduction to Vectors. Vector Examples. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Orthogonal Complements. Rank(A) = Rank(transpose of A). dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Showing that A-transpose x A is invertible. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes.

Sal does the 80 problems from the released questions from the California Standards Test for Geometry.

This course is an introduction to differential geometry. The course itself is mathematically rigorous, but still emphasizes concrete aspects of geometry, centered on the notion of curvature.

8.962 is MIT's graduate course in general relativity, which covers the basic principles of Einstein's general theory of relativity, differential geometry, experimental tests of general relativity, black holes, and cosmology.

The ACT (American College Testing) is a standardized test for high school achievement and college admissions in the United States produced by ACT, Inc. The ACT test has historically consisted of four tests: English, Mathematics, Reading, and Science Reasoning. The 60-question math test consists of 14 questions covering pre-algebra, 10 elementary algebra, 9 intermediate algebra, 14 plane geometry, 9 coordinate geometry, and 4 elementary trigonometry. This free online course from ALISON contains 60 sample problems similar to the ones you will find in your own. This course is ideal for any learner studying for the ACT math exam.<br />

<p>This course is ideal for people who want to gain a thorough understanding and knowledge of advanced topics in algebra. </p><br /> <p>The advanced algebra topics include linear equations, inequalities, graphs, matrices, polynomials, radical expressions, quadratic equations, functions, exponential, logarithmic expressions, sequences, series, probability and trigonometry. </p> <br /> <p>The course is divided into 13 modules and each module is divided into lessons with theory, examples and video explanations, making for an enhanced study experience. </p>

This is the first semester of a two-semester sequence on Algebraic Geometry. The goal of the course is to introduce the basic notions and techniques of modern algebraic geometry. It covers fundamental notions and results about algebraic varieties over an algebraically closed field; relations between complex algebraic varieties and complex analytic varieties; and examples with emphasis on algebraic curves and surfaces. This course is an introduction to the language of schemes and properties of morphisms.

This research-oriented course will focus on algebraic and computational techniques for optimization problems involving polynomial equations and inequalities with particular emphasis on the connections with semidefinite optimization. The course will develop in a parallel fashion several algebraic and numerical approaches to polynomial systems, with a view towards methods that simultaneously incorporate both elements. We will study both the complex and real cases, developing techniques of general applicability, and stressing convexity-based ideas, complexity results, and efficient implementations. Although we will use examples from several engineering areas, particular emphasis will be given to those arising from systems and control applications.

This course is a review of Basic Arithmetic skills that serve as a prerequisite for placement into and success in pre-college and college-level algebra courses. In this course, primary emphasis will be placed on fundamental operations with whole numbers, fractions, decimals, and integers. Other topics covered include proportions, percentages, representations of data, geometric figures, and measurement. Students who should take this course include: those that have an interest in brushing up on arithmetic skills prior to taking an upcoming placement test or those that have not had math in many years and want to review foundational skills and concepts. This course provides free digital access to all required materials including a student workbook, lesson videos, and online homework practice and assessment. A certificate of completion will be awarded by the instructor to students who complete required activities. The course instructor recommends purchase of a textbook or other course materials. Please see the details below. Required materials: Basic Arithmetic Student Workbook Purchase Info: Hard copy at Lulu.com or access via free digital download. Approximate cost for hard copy: $15

This course offers an introduction to discrete and computational geometry. Emphasis is placed on teaching methods in combinatorial geometry. Many results presented are recent, and include open (as yet unsolved) problems.