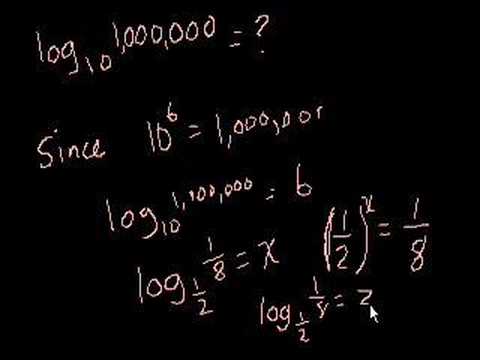Online courses directory (418)
Example problems from random math competitions. 2003 AIME II Problem 1. 2003 AIME II Problem 3. 2003 AIME II Problem 4 (part 1). Sum of factors of 27000. Sum of factors 2. 2003 AIME II Problem 5. 2003 AIME II Problem 5 Minor Correction. Area Circumradius Formula Proof. 2003 AIME II Problem 8. Sum of Polynomial Roots (Proof). Sum of Squares of Polynomial Roots. 2003 AIME II Problem 9. 2003 AIME II Problem 12. 2003 AIME II Problem 13. 2003 AIME II Problem 10. 2003 AIME II Problem 11. 2003 AIME II Problem 14. 2003 AIME II Problem 15 (part 1). 2003 AIME II Problem 15 (part 2). 2003 AIME II Problem 15 (part 3). 2003 AIME II Problem 1. 2003 AIME II Problem 3. 2003 AIME II Problem 4 (part 1). Sum of factors of 27000. Sum of factors 2. 2003 AIME II Problem 5. 2003 AIME II Problem 5 Minor Correction. Area Circumradius Formula Proof. 2003 AIME II Problem 8. Sum of Polynomial Roots (Proof). Sum of Squares of Polynomial Roots. 2003 AIME II Problem 9. 2003 AIME II Problem 12. 2003 AIME II Problem 13. 2003 AIME II Problem 10. 2003 AIME II Problem 11. 2003 AIME II Problem 14. 2003 AIME II Problem 15 (part 1). 2003 AIME II Problem 15 (part 2). 2003 AIME II Problem 15 (part 3).
In this topic, we'll analyze, graph and solve quadratic equations. Example 1: Solving a quadratic equation by factoring. Example 2: Solving a quadratic equation by factoring. Example 3: Solving a quadratic equation by factoring. Example 4: Solving a quadratic equation by factoring. Solving quadratics by factoring. Solving quadratics by factoring 2. Solving Quadratic Equations by Square Roots. Example: Solving simple quadratic. Solving quadratics by taking the square root. Solving Quadratic Equations by Completing the Square. Completing the square (old school). Example: Completing perfect square trinomials. Example 1: Completing the square. Example 2: Completing the square. Example 3: Completing the square. Example 4: Completing the square. Example 5: Completing the square. Completing the square 1. Completing the square 2. How to use the Quadratic Formula. Example: Quadratics in standard form. Proof of Quadratic Formula. Example 1: Using the quadratic formula. Example 2: Using the quadratic formula. Example 3: Using the quadratic formula. Example 4: Applying the quadratic formula. Example 5: Using the quadratic formula. Quadratic formula. Example: Complex roots for a quadratic. Quadratic formula with complex solutions. Discriminant of Quadratic Equations. Discriminant for Types of Solutions for a Quadratic. Solutions to quadratic equations. Graphing a parabola with a table of values. Parabola vertex and axis of symmetry. Graphing a parabola by finding the roots and vertex. Finding the vertex of a parabola example. Vertex of a parabola. Multiple examples graphing parabolas using roots and vertices. Graphing a parabola using roots and vertex. Graphing parabolas in standard form. Graphing a parabola in vertex form. Graphing parabolas in vertex form. Graphing parabolas in all forms. Parabola Focus and Directrix 1. Focus and Directrix of a Parabola 2. Using the focus and directrix to find the equation of a parabola. Parabola intuition 3. Quadratic Inequalities. Quadratic Inequalities (Visual Explanation). Solving a quadratic by factoring. CA Algebra I: Factoring Quadratics. Algebra II: Quadratics and Shifts. Examples: Graphing and interpreting quadratics. CA Algebra I: Completing the Square. Introduction to the quadratic equation. Quadratic Equation part 2. Quadratic Formula (proof). CA Algebra I: Quadratic Equation. CA Algebra I: Quadratic Roots. Example 1: Solving a quadratic equation by factoring. Example 2: Solving a quadratic equation by factoring. Example 3: Solving a quadratic equation by factoring. Example 4: Solving a quadratic equation by factoring. Solving quadratics by factoring. Solving quadratics by factoring 2. Solving Quadratic Equations by Square Roots. Example: Solving simple quadratic. Solving quadratics by taking the square root. Solving Quadratic Equations by Completing the Square. Completing the square (old school). Example: Completing perfect square trinomials. Example 1: Completing the square. Example 2: Completing the square. Example 3: Completing the square. Example 4: Completing the square. Example 5: Completing the square. Completing the square 1. Completing the square 2. How to use the Quadratic Formula. Example: Quadratics in standard form. Proof of Quadratic Formula. Example 1: Using the quadratic formula. Example 2: Using the quadratic formula. Example 3: Using the quadratic formula. Example 4: Applying the quadratic formula. Example 5: Using the quadratic formula. Quadratic formula. Example: Complex roots for a quadratic. Quadratic formula with complex solutions. Discriminant of Quadratic Equations. Discriminant for Types of Solutions for a Quadratic. Solutions to quadratic equations. Graphing a parabola with a table of values. Parabola vertex and axis of symmetry. Graphing a parabola by finding the roots and vertex. Finding the vertex of a parabola example. Vertex of a parabola. Multiple examples graphing parabolas using roots and vertices. Graphing a parabola using roots and vertex. Graphing parabolas in standard form. Graphing a parabola in vertex form. Graphing parabolas in vertex form. Graphing parabolas in all forms. Parabola Focus and Directrix 1. Focus and Directrix of a Parabola 2. Using the focus and directrix to find the equation of a parabola. Parabola intuition 3. Quadratic Inequalities. Quadratic Inequalities (Visual Explanation). Solving a quadratic by factoring. CA Algebra I: Factoring Quadratics. Algebra II: Quadratics and Shifts. Examples: Graphing and interpreting quadratics. CA Algebra I: Completing the Square. Introduction to the quadratic equation. Quadratic Equation part 2. Quadratic Formula (proof). CA Algebra I: Quadratic Equation. CA Algebra I: Quadratic Roots.
Understanding absolute value and solving absolute value equations and inequalities. Absolute Value and Number Lines. Absolute Value 1. Absolute Value of Integers. Comparing Absolute Values. CA Algebra I: Number Properties and Absolute Value. Absolute Value Equations. Absolute Value Equations Example 1. Absolute Value Equation Example 2. U02_L2_T2_we1 Absolute Value Equations.avi. Absolute Value Inequalities. Absolute value inequalities Example 1. Absolute Inequalities 2. Absolute value inequalities example 3.
Learn how to think the way mathematicians do - a powerful cognitive process developed over thousands of years.
Understanding and solving logarithms, including natural logs. Introduction to Logarithms. Logarithm of a Power. Sum of Logarithms with Same Base. Introduction to logarithm properties. Introduction to logarithm properties (part 2). Using Multiple Logarithm Properties to Simplify. Change of Base Formula. Logarithmic Scale. Richter Scale. Logarithmic Equations. Solving Logarithmic Equations. Proof: log a + log b = log ab. Proof: log_a (B) = (log_x (B))/(log_x (A)). Proof: A(log B) = log (B^A), log A - log B = log (A/B). Natural Logarithm with a Calculator. Calculator for Natural Logarithms. Graphing Natural Logarithm Function.
A broad set of tutorials covering perimeter area and volume with and without algebra. Perimeter and Area Basics. Area and Perimeter. Perimeter of a Polygon. Perimeter of a shape. Perimeter 1. Finding dimensions given perimeter. Area 1. Finding dimensions given area. Perimeter and Area Basics. Triangle Area Proofs. Area of triangles. Interesting Perimeter and Area Problems. Area of Diagonal Generated Triangles of Rectangle are Equal. Area of an equilateral triangle. Area of shaded region made from equilateral triangles. Shaded areas. Challenging Perimeter Problem. Triangle inqequality theorem. Triangle inequality theorem. Koch Snowflake Fractal. Area of an equilateral triangle. Area of Koch Snowflake (part 1) - Advanced. Area of Koch Snowflake (part 2) - Advanced. Heron's Formula. Heron's formula. Part 1 of Proof of Heron's Formula. Part 2 of the Proof of Heron's Formula. Circles: Radius, Diameter and Circumference. Parts of a Circle. Radius diameter and circumference. Area of a Circle. Area of a circle. Quadrilateral Overview. Quadrilateral Properties. Area of a Parallelogram. Area of parallelograms. Area of a trapezoid. Area of a kite. Area of trapezoids, rhombi, and kites. Perimeter of a Polygon. Perimeter and Area of a Non-Standard Polygon. How we measure volume. Measuring volume with unit cubes. Volume with unit cubes. Measuring volume as area times length. Volume of a rectangular prism or box examples. Volume 1. Volume word problem example. Volume word problems. Solid Geometry Volume. Cylinder Volume and Surface Area. Volume of a Sphere. Solid geometry. Perimeter and Area Basics. Area and Perimeter. Perimeter of a Polygon. Perimeter of a shape. Perimeter 1. Finding dimensions given perimeter. Area 1. Finding dimensions given area. Perimeter and Area Basics. Triangle Area Proofs. Area of triangles. Interesting Perimeter and Area Problems. Area of Diagonal Generated Triangles of Rectangle are Equal. Area of an equilateral triangle. Area of shaded region made from equilateral triangles. Shaded areas. Challenging Perimeter Problem. Triangle inqequality theorem. Triangle inequality theorem. Koch Snowflake Fractal. Area of an equilateral triangle. Area of Koch Snowflake (part 1) - Advanced. Area of Koch Snowflake (part 2) - Advanced. Heron's Formula. Heron's formula. Part 1 of Proof of Heron's Formula. Part 2 of the Proof of Heron's Formula. Circles: Radius, Diameter and Circumference. Parts of a Circle. Radius diameter and circumference. Area of a Circle. Area of a circle. Quadrilateral Overview. Quadrilateral Properties. Area of a Parallelogram. Area of parallelograms. Area of a trapezoid. Area of a kite. Area of trapezoids, rhombi, and kites. Perimeter of a Polygon. Perimeter and Area of a Non-Standard Polygon. How we measure volume. Measuring volume with unit cubes. Volume with unit cubes. Measuring volume as area times length. Volume of a rectangular prism or box examples. Volume 1. Volume word problem example. Volume word problems. Solid Geometry Volume. Cylinder Volume and Surface Area. Volume of a Sphere. Solid geometry.
California Standards Test: Algebra II. California Standards Test: Algebra II (Graphing Inequalities). CA Standards: Algebra II (Algebraic Division/Multiplication). CA Standards: Algebra II. Algebra II: Simplifying Polynomials. Algebra II: Imaginary and Complex Numbers. Algebra II: Complex numbers and conjugates. Algebra II: Quadratics and Shifts. Examples: Graphing and interpreting quadratics. Hyperbola and parabola examples. Algebra II: Circles and Logarithms. Algebra II: Logarithms Exponential Growth. Algebra II: Logarithms and more. Algebra II: Functions, Combinatorics. Algebra II: binomial Expansion and Combinatorics. Algebra II: Binomial Expansions, Geometric Series Sum. Algebra II: Functions and Probability. Algebra II: Probability and Statistics. Algebra II: Mean and Standard Deviation.
Understanding the purpose, notation, and building blocks of geometry. Euclid as the Father of Geometry. Language and Notation of Basic Geometry. Lines, Line Segments, and Rays. Identifying Rays. Identifying Parallel and Perpendicular Lines.
Understanding and solving exponents without algebra. Understanding Exponents. Understanding Exponents 2. Level 1 Exponents. Level 2 Exponents. Level 3 exponents. Exponent Rules Part 1. Exponent Rules Part 2.
Learn about General Game Playing (GGP) and develop GGP programs capable of competing against humans and other programs in GGP competitions .
This course teaches a calculus that enables precise quantitative predictions of large combinatorial structures. Part I covers generating functions and real asymptotics and then introduces the symbolic method in the context of applications in the analysis of algorithms and basic structures such as permutations, trees, strings, words, and mappings.
This class presents the fundamental probability and statistical concepts used in elementary data analysis. It will be taught at an introductory level for students with junior or senior college-level mathematical training including a working knowledge of calculus. A small amount of linear algebra and programming are useful for the class, but not required.
Understanding and finding factors and multiples. After these videos, you'll be ready for fractions. Divisibility Tests for 2, 3, 4, 5, 6, 9, 10. Recognizing Divisibility. The Why of the 3 Divisibility Rule. The Why of the 9 Divisibility Rule. Divisibility tests. Finding Factors of a Number. Finding factors and multiples. Divisibility 0.5. Divisibility Intuition. Divisibility intuition. Prime Numbers. Recognizing Prime Numbers. Prime numbers. Composite numbers. Prime Factorization. Prime factorization exercise. Prime factorization. The fundamental theorem of arithmetic. The fundamental theorem of arithmetic. Common Divisibility Examples. Divisibility. Least common multiple exercise. Least common multiple exercise 2. Least Common Multiple (LCM). Old Least Common Multiple. Least common multiple. Greatest common divisor factor exercise. Greatest Common Divisor. Greatest common divisor. LCM and GCF (greatest common factor) word problems. LCM and GCD word problems. Divisibility Tests for 2, 3, 4, 5, 6, 9, 10. Recognizing Divisibility. The Why of the 3 Divisibility Rule. The Why of the 9 Divisibility Rule. Divisibility tests. Finding Factors of a Number. Finding factors and multiples. Divisibility 0.5. Divisibility Intuition. Divisibility intuition. Prime Numbers. Recognizing Prime Numbers. Prime numbers. Composite numbers. Prime Factorization. Prime factorization exercise. Prime factorization. The fundamental theorem of arithmetic. The fundamental theorem of arithmetic. Common Divisibility Examples. Divisibility. Least common multiple exercise. Least common multiple exercise 2. Least Common Multiple (LCM). Old Least Common Multiple. Least common multiple. Greatest common divisor factor exercise. Greatest Common Divisor. Greatest common divisor. LCM and GCF (greatest common factor) word problems. LCM and GCD word problems.
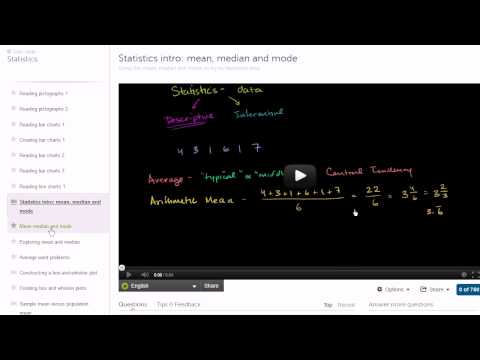
Introduction to statistics. We start with the basics of reading and interpretting data and then build into descriptive and inferential statistics that are typically covered in an introductory course on the subject. Overview of Khan Academy statistics. Statistics intro: mean, median and mode. Constructing a box-and-whisker plot. Sample mean versus population mean.. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Statistics: Standard Deviation. Statistics: Alternate Variance Formulas. Introduction to Random Variables. Probability Density Functions. Binomial Distribution 1. Binomial Distribution 2. Binomial Distribution 3. Binomial Distribution 4. Expected Value: E(X). Expected Value of Binomial Distribution. Poisson Process 1. Poisson Process 2. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. Law of Large Numbers. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. ck12.org: More Empirical Rule and Z-score practice. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Small Sample Size Confidence Intervals. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Z-statistics vs. T-statistics. Type 1 Errors. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Squared Error of Regression Line. Proof (Part 1) Minimizing Squared Error to Regression Line. Proof Part 2 Minimizing Squared Error to Line. Proof (Part 3) Minimizing Squared Error to Regression Line. Proof (Part 4) Minimizing Squared Error to Regression Line. Regression Line Example. Second Regression Example. R-Squared or Coefficient of Determination. Calculating R-Squared. Covariance and the Regression Line. Correlation and Causality. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Mean Median and Mode. Range and Mid-range. Reading Pictographs. Reading Bar Graphs. Reading Line Graphs. Reading Pie Graphs (Circle Graphs). Misleading Line Graphs. Stem-and-leaf Plots. Box-and-Whisker Plots. Reading Box-and-Whisker Plots. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance. Deductive Reasoning 1. Deductive Reasoning 2. Deductive Reasoning 3. Inductive Reasoning 1. Inductive Reasoning 2. Inductive Reasoning 3. Inductive Patterns.
Solving and writing algebraic ratios and proportions. Solving rational equations. Introduction to Ratios (new HD version). Understanding Proportions. Ratios as Fractions in Simplest Form. Simplifying Rates and Ratios. Find an Unknown in a Proportion. Ratio and Proportion. Find an Unknown in a Proportion 2. Another Take on the Rate Problem. Finding Unit Rates. Finding Unit Prices. Writing Proportions. Ratio problem with basic algebra (new HD). More advanced ratio problem--with Algebra (HD version). Alternate Solution to Ratio Problem (HD Version). Advanced ratio problems. Unit conversion. Conversion between metric units. Converting within the metric system. Converting pounds to ounces. Converting Gallons to quarts pints and cups. Converting Farenheit to Celsius. Comparing Celsius and Farenheit temperature scales. Applying the Metric System. U.S. Customary and Metric units. Converting Yards into Inches. Unit Conversion with Fractions. Performing arithmetic calculations on units of volume. Application problems involving units of weight. Solving application problems involving units of volume. Unit Conversion Example: Drug Dosage. Perimeter and Unit Conversion. Rational Equations. Solving Rational Equations 1. Solving Rational Equations 2. Solving Rational Equations 3. Applying Rational Equations 1. Applying Rational Equations 2. Applying Rational Equations 3. Extraneous Solutions to Rational Equations. Rational Inequalities 2.
Defining and using the commutative, associative, distributive, identity, and inverse properties. Commutative Law of Addition. Commutative Law of Multiplication. Associative Law of Addition. Associative Law of Multiplication. Commutative Property for Addition. The Distributive Property. The Distributive Property 2. Distributive Property Example 1. CA Algebra I: Number Properties and Absolute Value. Identity Property of 1. Identity property of 1 (second example). Identity property of 0. Inverse Property of Addition. Inverse Property of Multiplication. Why Dividing by Zero is Undefined. Why Zero Divided by Zero is Undefined/Indeterminate. Undefined and Indeterminate.
Solving and writing ratios and proportions without algebra. Introduction to Ratios (new HD version). Understanding Proportions. Ratios as Fractions in Simplest Form. Simplifying Rates and Ratios. Find an Unknown in a Proportion 2. Finding Unit Rates. Finding Unit Prices. Unit conversion. Converting units of length. Conversion between metric units. U.S. Customary and Metric units. Converting within the metric system. Converting Gallons to quarts pints and cups. Converting pounds to ounces. Comparing Celsius and Farenheit temperature scales. Converting Fahrenheit to Celsius. Speed translation.
Identifying types of quadrilaterals, finding measurements, and applying and proving postulates. Quadrilateral Overview. Quadrilateral Properties. Area of a Parallelogram. Area of a Regular Hexagon. Sum of Interior Angles of a Polygon. Sum of the exterior angles of convex polygon. Proof - Opposite Angles of Parallelogram Congruent. Proof - Opposite Sides of Parallelogram Congruent. Proof - Diagonals of a Parallelogram Bisect Each Other. Rhombus Diagonals. Proof - Rhombus Diagonals are Perpendicular Bisectors. Proof - Rhombus Area Half Product of Diagonal Length. Area of a Parallelogram. Area of a Regular Hexagon. Problem involving angle derived from square and circle. 2003 AIME II Problem 7. CA Geometry: Deducing Angle Measures.
Random logic puzzles and brain teasers. Fun to do and useful for many job interviews!. Liar Truth-teller Brain Teaser. Toggler Brain Teaser. Alien Abduction Brain Teaser. Blue Forehead Room Brain Teaser. Blue Forehead Room Solution. Forehead Numbers Brain Teaser. Light Bulb Switching Brain Teaser. Path Counting Brain Teaser. 3-D Path Counting Brain Teaser. Liar Truth-teller Brain Teaser. Toggler Brain Teaser. Alien Abduction Brain Teaser. Blue Forehead Room Brain Teaser. Blue Forehead Room Solution. Forehead Numbers Brain Teaser. Light Bulb Switching Brain Teaser. Path Counting Brain Teaser. 3-D Path Counting Brain Teaser.
Identifying, solving, and graphing various types of functions. What is a function. Difference between Equations and Functions. Function example problems. Ex: Constructing a function. Understanding Function Notation Example 1). Understanding Function Notation Example 2). Understanding Function Notation Example 3). Understanding function notation. Testing if a relationship is a function. Graphical Relations and Functions. Functions as Graphs. Recognizing functions (example 1). Recognizing functions (example 2). Recognizing functions. Relations and Functions. Functional Relationships 1. Recognizing functions (example 3). Recognizing functions (example 4). Recognizing functions (example 5). Recognizing functions 2. Domain of a function. Domain and Range of a Relation. Domain and Range of a Function Given a Formula. Domain and Range 1. Domain of a Radical Function. Domain of a function. Domain and Range 2. Domain and Range of a Function. Range of a function. Domain and range from graphs. Domain and range from graph. Direct and Inverse Variation. Recognizing Direct and Inverse Variation. Proportionality Constant for Direct Variation. Direct and inverse variation. Direct Variation Models. Direct Variation 1. Inverse Variation Application. Direct Inverse and Joint Variation. Direct Variation Application. Ex 1: Evaluating a function. Ex 2: Graphing a basic function. Graphing a parabola with a table of values. Ex 4: Graphing radical functions. Ex: Graphing exponential functions. Views of a function. Interpreting a graph exercise example. Interpreting graphs of linear and nonlinear functions. Quotient of Functions. Sum of Functions. Product of Functions. Difference of Functions. Evaluating a function expression. Evaluating expressions with function notation. Evaluating composite functions example. Evaluating composite functions. Introduction to Function Inverses. Function Inverse Example 1. Function Inverses Example 2. Function Inverses Example 3. Inverses of functions. New operator definitions. New operator definitions 1. New operator definitions 2. New operator definitions 2. Introduction to functions. Functions Part 2. Functions (Part III). Functions (part 4). What is a function. Difference between Equations and Functions. Function example problems. Ex: Constructing a function. Understanding Function Notation Example 1). Understanding Function Notation Example 2). Understanding Function Notation Example 3). Understanding function notation. Testing if a relationship is a function. Graphical Relations and Functions. Functions as Graphs. Recognizing functions (example 1). Recognizing functions (example 2). Recognizing functions. Relations and Functions. Functional Relationships 1. Recognizing functions (example 3). Recognizing functions (example 4). Recognizing functions (example 5). Recognizing functions 2. Domain of a function. Domain and Range of a Relation. Domain and Range of a Function Given a Formula. Domain and Range 1. Domain of a Radical Function. Domain of a function. Domain and Range 2. Domain and Range of a Function. Range of a function. Domain and range from graphs. Domain and range from graph. Direct and Inverse Variation. Recognizing Direct and Inverse Variation. Proportionality Constant for Direct Variation. Direct and inverse variation. Direct Variation Models. Direct Variation 1. Inverse Variation Application. Direct Inverse and Joint Variation. Direct Variation Application. Ex 1: Evaluating a function. Ex 2: Graphing a basic function. Graphing a parabola with a table of values. Ex 4: Graphing radical functions. Ex: Graphing exponential functions. Views of a function. Interpreting a graph exercise example. Interpreting graphs of linear and nonlinear functions. Quotient of Functions. Sum of Functions. Product of Functions. Difference of Functions. Evaluating a function expression. Evaluating expressions with function notation. Evaluating composite functions example. Evaluating composite functions. Introduction to Function Inverses. Function Inverse Example 1. Function Inverses Example 2. Function Inverses Example 3. Inverses of functions. New operator definitions. New operator definitions 1. New operator definitions 2. New operator definitions 2. Introduction to functions. Functions Part 2. Functions (Part III). Functions (part 4).
Trusted paper writing service WriteMyPaper.Today will write the papers of any difficulty.