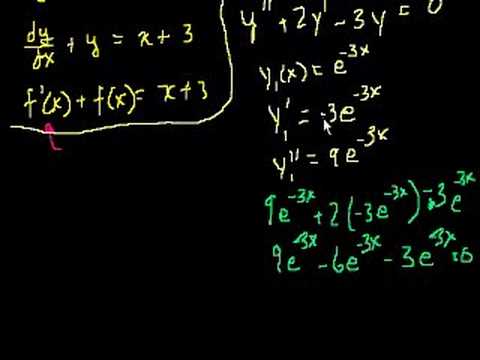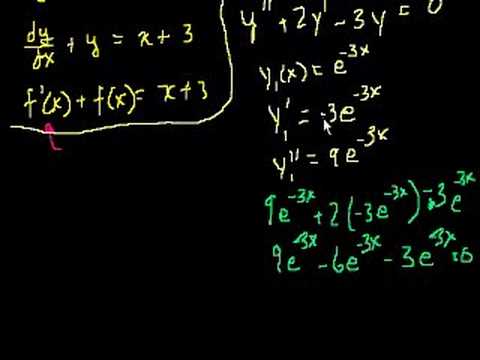Online courses directory (418)

During this four week course, instructors will learn how to create and teach an exciting new type of developmental math course known as a pathways course. These courses (e.g., Math Literacy for College Students, Quantway

This course is designed to introduce you to the study of Calculus.  You will learn concrete applications of how calculus is used and, more importantly, why it works.  Calculus is not a new discipline; it has been around since the days of Archimedes.  However, Isaac Newton and Gottfried Leibniz, two 17th-century European mathematicians concurrently working on the same intellectual discovery hundreds of miles apart, were responsible for developing the field as we know it today.  This brings us to our first question, what is today's Calculus?  In its simplest terms, calculus is the study of functions, rates of change, and continuity.  While you may have cultivated a basic understanding of functions in previous math courses, in this course you will come to a more advanced understanding of their complexity, learning to take a closer look at their behaviors and nuances. In this course, we will address three major topics: limits, derivatives, and integrals, as well as study their respective foundations and a…

This course is the second installment of Single-Variable Calculus.  In Part I (MA101) [1], we studied limits, derivatives, and basic integrals as a means to understand the behavior of functions.  In this course (Part II), we will extend our differentiation and integration abilities and apply the techniques we have learned. Additional integration techniques, in particular, are a major part of the course.  In Part I, we learned how to integrate by various formulas and by reversing the chain rule through the technique of substitution.  In Part II, we will learn some clever uses of substitution, how to reverse the product rule for differentiation through a technique called integration by parts, and how to rewrite trigonometric and rational integrands that look impossible into simpler forms.  Series, while a major topic in their own right, also serve to extend our integration reach: they culminate in an application that lets you integrate almost any function you’d like. Integration allows us to calculat…

This course is an introduction to linear algebra.  It has been argued that linear algebra constitutes half of all mathematics.  Whether or not everyone would agree with that, it is certainly true that practically every modern technology relies on linear algebra to simplify the computations required for Internet searches, 3-D animation, coordination of safety systems, financial trading, air traffic control, and everything in between. Linear algebra can be viewed either as the study of linear equations or as the study of vectors.  It is tied to analytic geometry; practically speaking, this means that almost every fact you will learn in this course has a picture associated with it.  Learning to connect the facts with their geometric interpretation will be very useful for you. The book which is used in the course focuses both on the theoretical aspects as well as the applied aspects of linear algebra.  As a result, you will be able to learn the geometric interpretations of many of the algebraic concepts…

In this course, you will look at the properties behind the basic concepts of probability and statistics and focus on applications of statistical knowledge.  You will learn about how statistics and probability work together.  The subject of statistics involves the study of methods for collecting, summarizing, and interpreting data.  Statistics formalizes the process of making decisions, and this course is designed to help you use statistical literacy to make better decisions.  Note that this course has applications for the natural sciences, economics, computer science, finance, psychology, sociology, criminology, and many other fields. We read data in articles and reports every day.  After finishing this course, you should be comfortable evaluating an author's use of data.  You will be able to extract information from articles and display that information effectively.  You will also be able to understand the basics of how to draw statistical conclusions. This course will begin with descriptive statistic…

This course has been designed to provide you with a clear, accessible introduction to discrete mathematics. Discrete mathematics describes processes that consist of a sequence of individual steps (as compared to calculus, which describes processes that change in a continuous manner). The principal topics presented in this course are logic and proof, induction and recursion, discrete probability, and finite state machines. As you progress through the units of this course, you will develop the mathematical foundations necessary for more specialized subjects in computer science, including data structures, algorithms, and compiler design. Upon completion of this course, you will have the mathematical know-how required for an in-depth study of the science and technology of the computer age.

Build your earth science vocabulary and learn about cycles of matter and types of sedimentary rocks through the Education Portal course Earth Science 101: Earth Science. Our series of video lessons and accompanying self-assessment quizzes can help you boost your scientific knowledge ahead of the Excelsior Earth Science exam . This course was designed by experienced educators and examines both science basics, like experimental design and systems of measurement, and more advanced topics, such as analysis of rock deformation and theories of continental drift.

Build your earth science vocabulary and learn about cycles of matter and types of sedimentary rocks through the Education Portal course Earth Science 101: Earth Science. Our series of video lessons and accompanying self-assessment quizzes can help you boost your scientific knowledge ahead of the Excelsior Earth Science exam . This course was designed by experienced educators and examines both science basics, like experimental design and systems of measurement, and more advanced topics, such as analysis of rock deformation and theories of continental drift.

Build your earth science vocabulary and learn about cycles of matter and types of sedimentary rocks through the Education Portal course Earth Science 101: Earth Science. Our series of video lessons and accompanying self-assessment quizzes can help you boost your scientific knowledge ahead of the Excelsior Earth Science exam . This course was designed by experienced educators and examines both science basics, like experimental design and systems of measurement, and more advanced topics, such as analysis of rock deformation and theories of continental drift.

This is the first semester of a two-semester sequence on Differential Analysis. Topics include fundamental solutions for elliptic; hyperbolic and parabolic differential operators; method of characteristics; review of Lebesgue integration; distributions; fourier transform; homogeneous distributions; asymptotic methods.

In this course, we study elliptic Partial Differential Equations (PDEs) with variable coefficients building up to the minimal surface equation. Then we study Fourier and harmonic analysis, emphasizing applications of Fourier analysis. We will see some applications in combinatorics / number theory, like the Gauss circle problem, but mostly focus on applications in PDE, like the Calderon-Zygmund inequality for the Laplacian, and the Strichartz inequality for the Schrodinger equation. In the last part of the course, we study solutions to the linear and the non-linear Schrodinger equation. All through the course, we work on the craft of proving estimates.

The laws of nature are expressed as differential equations. Scientists and engineers must know how to model the world in terms of differential equations, and how to solve those equations and interpret the solutions. This course focuses on the equations and techniques most useful in science and engineering.

Course Format

This course has been designed for independent study. It provides everything you will need to understand the concepts covered in the course. The materials include:

• Lecture Videos by Professor Arthur Mattuck.
• Course Notes on every topic.
• Practice Problems with Solutions.
• Problem Solving Videos taught by experienced MIT Recitation Instructors.
• Problem Sets to do on your own with Solutions to check your answers against when you're done.
• A selection of Interactive Java® Demonstrations called Mathlets to illustrate key concepts.
• A full set of Exams with Solutions, including practice exams to help you prepare.

Content Development

Differential Equations are the language in which the laws of nature are expressed. Understanding properties of solutions of differential equations is fundamental to much of contemporary science and engineering. Ordinary differential equations (ODE's) deal with functions of one variable, which can often be thought of as time.

Topics covered in a first year course in differential equations. Need to understand basic differentiation and integration from Calculus playlist before starting here. What is a differential equation. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4. Laplace Transform 1. Laplace Transform 2. Laplace Transform 3 (L{sin(at)}). Laplace Transform 4. Laplace Transform 5. Laplace Transform 6. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. More Laplace Transform tools. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Laplace/Step Function Differential Equation. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob.

Topics covered in a first year course in differential equations.

Differential equations with only first derivatives. What is a differential equation. Simple Differential Equations. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2. What is a differential equation. Simple Differential Equations. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2.

Transforms and the Laplace transform in particular. Convolution integrals. Laplace Transform 1. Laplace Transform 2. L{sin(at)}) - transform of sin(at). Part 2 of the transform of the sin(at). Laplace as linear operator and Laplace of derivatives. Laplace Transform of cos t and polynomials. "Shifting" transform by multiplying function by exponential. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace/Step Function Differential Equation. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob. Laplace Transform 1. Laplace Transform 2. L{sin(at)}) - transform of sin(at). Part 2 of the transform of the sin(at). Laplace as linear operator and Laplace of derivatives. Laplace Transform of cos t and polynomials. "Shifting" transform by multiplying function by exponential. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace/Step Function Differential Equation. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob.

Linear differential equations that contain second derivatives. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4.

This course is an introduction to differential geometry. The course itself is mathematically rigorous, but still emphasizes concrete aspects of geometry, centered on the notion of curvature.

This intermediate math course continues our free online maths suite of courses. It covers rules and applications of differentiation, straight line graphs, graphing circular functions, logs and indices, the Binomial theorem, inverse functions, and factors of polynomials. This course is ideal for second-level students, anyone studying for an exam, and those interested in re-igniting their knowledge of mathematics!<br />