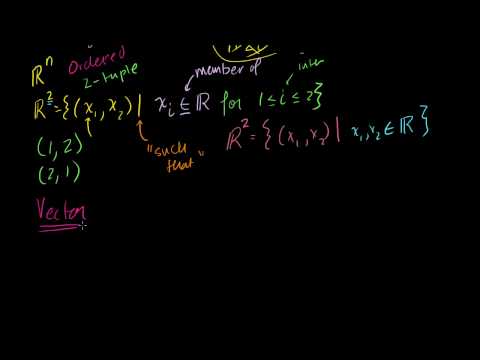Online courses directory (418)

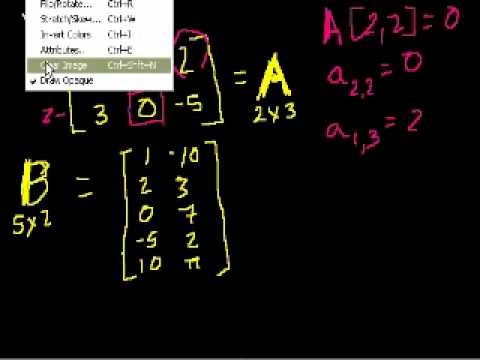
Matrices, vectors, vector spaces, transformations. Covers all topics in a first year college linear algebra course. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra. Introduction to matrices. Matrix multiplication (part 1). Matrix multiplication (part 2). Idea Behind Inverting a 2x2 Matrix. Inverting matrices (part 2). Inverting Matrices (part 3). Matrices to solve a system of equations. Matrices to solve a vector combination problem. Singular Matrices. 3-variable linear equations (part 1). Solving 3 Equations with 3 Unknowns. Introduction to Vectors. Vector Examples. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Orthogonal Complements. Rank(A) = Rank(transpose of A). dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Showing that A-transpose x A is invertible. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes.

This is a communication intensive supplement to Linear Algebra (18.06). The main emphasis is on the methods of creating rigorous and elegant proofs and presenting them clearly in writing. The course starts with the standard linear algebra syllabus and eventually develops the techniques to approach a more advanced topic: abstract root systems in a Euclidean space.

We explore creating and moving between various coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems.

Understanding how we can map one set of vectors to another set. Matrices used to define linear transformations. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible.

Let's get our feet wet by thinking in terms of vectors and spaces. Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A).

The course is an introduction to linear and discrete optimization - an important part of computational mathematics with a wide range of applications in many areas of everyday life.

This course will cover the very basic ideas in optimization. Topics include the basic theory and algorithms behind linear and integer linear programming along with some of the important applications. We will also explore the theory of convex polyhedra using linear programming.

This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite matrix problems. Numerics focus on finite-difference and finite-element techniques to reduce PDEs to matrix problems. The Julia Language (a free, open-source environment) is introduced and used in homework for simple examples.

Logic is a remarkable discipline. It is deeply tied to mathematics and philosophy, as correctness of argumentation is particularly crucial for these abstract disciplines. Logic systematizes and analyzes steps in reasoning: correct steps guarantee the truth of their conclusion given the truth of their premise(s); incorrect steps allow the formulation of counterexamples, i.e., of situations in which the premises are true, but the conclusion is false. Recognizing (and having conceptual tools for recognizing) the correctness or incorrectness of steps is crucial in order to critically evaluate arguments, not just in philosophy and mathematics, but also in ordinary life. This skill is honed by working in two virtual labs. In the ProofLab you learn to construct complex arguments in a strategically guided way, whereas in the TruthLab the emphasis is on finding counterexamples systematically. Who Should Take This Course? This is an introductory course designed for students from a broad range of disciplines, from mathematics and computer science to drama and creative writing. The highly interactive presentation makes it possible for any student to master the material. Concise multimedia lectures introduce each chapter; they discuss, in detail, the central notions and techniques presented in the text, but also articulate and motivate the learning objectives for each chapter. Open & Free Version The Open & Free, Logic & Proofs course includes the first five chapters of Logic & Proofs, providing a basic introduction to sentential logic. A full version of Logic & Proofs, including both sentential and predicate logic, is also available without technical or instructor support to independent users, for a small fee. No credit is awarded for completing either the Open & Free, Logic & Proofs course or the full, unsupported Logic & Proofs course. Academic Version Academic use of Logic & Proofs provides a full course on modern symbolic logic, covering both sentential and predicate logic, with identity. Optional suites of exams are available for use in academic sections.

This course begins with an introduction to the theory of computability, then proceeds to a detailed study of its most illustrious result: Kurt Gödel's theorem that, for any system of true arithmetical statements we might propose as an axiomatic basis for proving truths of arithmetic, there will be some arithmetical statements that we can recognize as true even though they don't follow from the system of axioms. In my opinion, which is widely shared, this is the most important single result in the entire history of logic, important not only on its own right but for the many applications of the technique by which it's proved. We'll discuss some of these applications, among them: Church's theorem that there is no algorithm for deciding when a formula is valid in the predicate calculus; Tarski's theorem that the set of true sentence of a language isn't definable within that language; and Gödel's second incompleteness theorem, which says that no consistent system of axioms can prove its own consistency.

This is an introduction to formal logic and how it is applied in computer science, electronic engineering, linguistics and philosophy. You will learn propositional logic—its language, interpretations and proofs, and apply it to solve problems in a wide range of disciplines.

This is an introduction to predicate logic and how it is applied in computer science, electronic engineering, linguistics, mathematics and philosophy. Building on your knowledge of propositional logic, you will learn predicate logic—its language, interpretations and proofs, and apply it to solve problems in a wide range of disciplines.

In this course, you will study basic algebraic operations and concepts, as well as the structure and use of algebra. This includes solving algebraic equations, factoring algebraic expressions, working with rational expressions, and graphing linear equations. You will apply these skills to solve real-world problems (word problems). Each unit will have its own application problems, depending on the concepts you have been exposed to. This course is also intended to provide you with a strong foundation for intermediate algebra and beyond. It will begin with a review of some math concepts formed in pre-algebra, such as ordering operations and simplifying simple algebraic expressions, to get your feet wet. You will then build on these concepts by learning more about functions, graphing of functions, evaluation of functions, and factorization. You will spend time on the rules of exponents and their applications in distribution of multiplication over addition/subtraction. This course provides students the opportuni…

Precalculus I is designed to prepare you for Precalculus II, Calculus, Physics, and higher math and science courses. In this course, the main focus is on five types of functions: linear, polynomial, rational, exponential, and logarithmic. In accompaniment with these functions, you will learn how to solve equations and inequalities, graph, find domains and ranges, combine functions, and solve a multitude of real-world applications. In this course, you will not only be learning new algebraic techniques that are necessary for other math and science courses, but you will be learning to become a critical thinker. You will be able to determine what is the best approach to take such as numerical, graphical, or algebraic to solve a problem given particular information. Then you will investigate and solve the problem, interpret the answer, and determine if it is reasonable. A few examples of applications in this course are determining compound interest, growth of bacteria, decay of a radioactive substance, and the…

Precalculus II continues the in-depth study of functions addressed in Precalculus I by adding the trigonometric functions to your function toolkit. In this course, you will cover families of trigonometric functions, as well as their inverses, properties, graphs, and applications. Additionally, you will study trigonometric equations and identities, the laws of sines and cosines, polar coordinates and graphs, parametric equations and elementary vector operations. You might be curious how the study of trigonometry, or “trig,” as it is more often referred to, came about and why it is important to your studies still. Trigonometry, from the Greek for “triangle measure,” studies the relationships between the angles of a triangle and its sides and defines the trigonometric functions used to describe those relationships. Trigonometric functions are particularly useful when describing cyclical phenomena and have applications in numerous fields, including astronomy, navigation, music theory, physics, chemistry…

This course is a continuation of MA001: Beginning Algebra [1]. Algebra allows us to formulate real-world problems in an abstract mathematical term or equation. These equations can then be solved by using techniques you will learn in this course. For example, if I can ride my bicycle at 5 miles per hour and I live 12 miles from work, how long will it take me to get to work? Or, suppose I am a pitcher for the St. Louis Cardinals and my fast ball is 95 miles per hour, how much time does the hitter have to react to the baseball? And, can you explain why an object thrown up into the air will come back down? If so, can you tell how long it will take for the object to hit the ground? These are all examples of problems that can be stated as an algebraic equation and then solved. In this course you will study compound inequalities and solve systems of linear equations. You will then study radicals and rational exponents, followed by quadratic equations and techniques used to solve these equations. Finally, you will…

Calculus can be thought of as the mathematics of CHANGE. Because everything in the world is changing, calculus helps us track those changes. Algebra, by contrast, can be thought of as dealing with a large set of numbers that are inherently CONSTANT. Solving an algebra problem, like y = 2x + 5, merely produces a pairing of two predetermined numbers, although an infinite set of pairs. Algebra is even useful in rate problems, such as calculating how the money in your savings account increases because of the interest rate R, such as Y = X0+Rt, where t is elapsed time and X0 is the initial deposit. With compound interest, things get complicated for algebra, as the rate R is itself a function of time with Y = X0 + R(t)t. Now we have a rate of change which itself is changing. Calculus came to the rescue, as Isaac Newton introduced the world to mathematics specifically designed to handle those things that change. Calculus is among the most important and useful developments of human thought. Even though it is over…

This course is designed to introduce you to the study of calculus. You will learn concrete applications of how calculus is used and, more importantly, why it works. Calculus is not a new discipline; it has been around since the days of Archimedes. However, Isaac Newton and Gottfried Leibniz, two seventeenth-century European mathematicians concurrently working on the same intellectual discovery hundreds of miles apart, were responsible for developing the field as we know it today. This brings us to our first question, what is today’s calculus? In its simplest terms, calculus is the study of functions, rates of change, and continuity. While you may have cultivated a basic understanding of functions in previous math courses, in this course you will come to a more advanced understanding of their complexity, learning to take a closer look at their behaviors and nuances. In this course, we will address three major topics: limits, derivatives, and integrals, as well as study their respective foundations and appl…

This course is designed to introduce you to the study of calculus.  You will learn concrete applications of how calculus is used and, more importantly, why it works.  Calculus is not a new discipline; it has been around since the days of Archimedes.  However, Isaac Newton and Gottfried Leibniz, two 17th century European mathematicians concurrently working on the same intellectual discovery hundreds of miles apart, were responsible for developing the field as we know it today.  This brings us to our first question, what is calculus today?  In its simplest terms, calculus is the study of functions, rates of change, and continuity.  While you may have cultivated a basic understanding of functions in previous math courses, in this course you will come to a more advanced understanding of their complexity, learning to take a closer look at their behaviors and nuances. In this course, we will address three major topics: limits, derivatives, and integrals, as well as study their respective foundations and ap…

This course is the second installment of Single-Variable Calculus.  In Part I (MA101) [1], we studied limits, derivatives, and basic integrals as a means to understand the behavior of functions.  In this course (Part II), we will extend our differentiation and integration abilities and apply the techniques we have learned. Additional integration techniques, in particular, are a major part of the course.  In Part I, we learned how to integrate by various formulas and by reversing the chain rule through the technique of substitution.  In Part II, we will learn some clever uses of substitution, how to reverse the product rule for differentiation through a technique called integration by parts, and how to rewrite trigonometric and rational integrands that look impossible into simpler forms.  Series, while a major topic in their own right, also serve to extend our integration reach: they culminate in an application that lets you integrate almost any function you’d like. Integration allows us to calculat…