Online courses directory (418)

Statistical Reasoning introduces students to the basic concepts and logic of statistical reasoning and gives the students introductory-level practical ability to choose, generate, and properly interpret appropriate descriptive and inferential methods. In addition, the course helps students gain an appreciation for the diverse applications of statistics and its relevance to their lives and fields of study. The course does not assume any prior knowledge in statistics and its only prerequisite is basic algebra. We offer two versions of statistics, each with a different emphasis: Probability and Statistics and Statistical Reasoning. Each course includes all expository text, simulations, case studies, comprehension tests, interactive learning exercises, and the StatTutor labs. Each course contains all of the instructions for the four statistics packages options we support. To do the activities, you will need your own copy of Microsoft Excel, Minitab, the open source R software, TI calculator, or StatCrunch. One of the main differences between the courses is the path through probability; Statistical Reasoning places less emphasis on probability than does the Probability and Statistics course and takes an empirical approach.

Introduction to statistics. Will eventually cover all of the major topics in a first-year statistics course.

We live in a time of unprecedented access to information. You'll learn how to use statistics to interpret that information and make decisions. San Jose State University

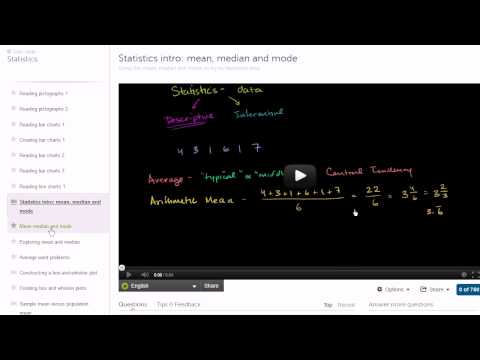
Introduction to statistics. We start with the basics of reading and interpretting data and then build into descriptive and inferential statistics that are typically covered in an introductory course on the subject. Overview of Khan Academy statistics. Statistics intro: mean, median and mode. Constructing a box-and-whisker plot. Sample mean versus population mean.. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Statistics: Standard Deviation. Statistics: Alternate Variance Formulas. Introduction to Random Variables. Probability Density Functions. Binomial Distribution 1. Binomial Distribution 2. Binomial Distribution 3. Binomial Distribution 4. Expected Value: E(X). Expected Value of Binomial Distribution. Poisson Process 1. Poisson Process 2. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. Law of Large Numbers. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. ck12.org: More Empirical Rule and Z-score practice. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Small Sample Size Confidence Intervals. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Z-statistics vs. T-statistics. Type 1 Errors. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Squared Error of Regression Line. Proof (Part 1) Minimizing Squared Error to Regression Line. Proof Part 2 Minimizing Squared Error to Line. Proof (Part 3) Minimizing Squared Error to Regression Line. Proof (Part 4) Minimizing Squared Error to Regression Line. Regression Line Example. Second Regression Example. R-Squared or Coefficient of Determination. Calculating R-Squared. Covariance and the Regression Line. Correlation and Causality. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Mean Median and Mode. Range and Mid-range. Reading Pictographs. Reading Bar Graphs. Reading Line Graphs. Reading Pie Graphs (Circle Graphs). Misleading Line Graphs. Stem-and-leaf Plots. Box-and-Whisker Plots. Reading Box-and-Whisker Plots. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance. Deductive Reasoning 1. Deductive Reasoning 2. Deductive Reasoning 3. Inductive Reasoning 1. Inductive Reasoning 2. Inductive Reasoning 3. Inductive Patterns.

This course is a broad treatment of statistics, concentrating on specific statistical techniques used in science and industry. Topics include: hypothesis testing and estimation, confidence intervals, chi-square tests, nonparametric statistics, analysis of variance, regression, correlation, decision theory, and Bayesian statistics.

Provides a firm grounding in the foundations of probability and statistics, the course focuses on real examples from the medical literature and popular press

Provides a firm grounding in the foundations of probability and statistics, the course focuses on real examples from the medical literature and popular press.

Statistics One is a comprehensive yet friendly introduction to statistics.

This free online course is the first of our Upper-Secondary Mathematics suite of courses. It covers mathematical analysis, including univariate statistics and data, bivariate statistics, correlation, regression, residual analysis, non-linear data, and seasonal movements. This course is suitable for students of maths, especially those preparing for examinations. It is also suitable for those looking to refresh their knowledge of Mathematics. <br />

This course is an introduction to the key ideas and principles of the collection, display, and analysis of data to guide you in making valid and appropriate conclusions about the world.

This course teaches the art of guessing results and solving problems without doing a proof or an exact calculation. Techniques include extreme-cases reasoning, dimensional analysis, successive approximation, discretization, generalization, and pictorial analysis. Applications include mental calculation, solid geometry, musical intervals, logarithms, integration, infinite series, solitaire, and differential equations. (No epsilons or deltas are harmed by taking this course.) This course is offered during the Independent Activities Period (IAP), which is a special 4-week term at MIT that runs from the first week of January until the end of the month.

在社会学、心理学、教育学、经济学、管理学、市场学等研究领域的数据分析中，结构方程建模是当前最前沿的统计方法中应用最广、研究最多的一个。它包含了方差分析、回归分析、路径分析和因子分析，弥补了传统回归分析和因子分析的不足，可以分析多因多果的联系、潜变量的关系，还可以处理多水平数据和纵向数据，是非常重要的多元数据分析工具。本课程系统地介绍结构方程模型和LISREL软件的应用，内容包括：结构方程分析（包括验证性因子分析）的基本概念、统计原理、在社会科学研究中的应用、常用模型及其LISREL程序、结果的解释和模型评价。学员应具备基本的统计知识（如：标准差、t-检验、相关系数），理解回归分析和因子分析的概念。 注：本课程配套教材为《结构方程模型及其应用》（以LISREL软件为例）。

The Statics of Everyday Objects is a course about how structures react to forces exerted on them while remaining unmoved.

The subject of enumerative combinatorics deals with counting the number of elements of a finite set. For instance, the number of ways to write a positive integer n as a sum of positive integers, taking order into account, is 2^n-1. We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them. This is a subject which requires little mathematical background to reach the frontiers of current research. Students will therefore have the opportunity to do original research. It might be necessary to limit enrollment.

The key learning objectives of this MOOC are: 1. Review, develop, and demonstrate their conceptual understanding and procedural skills with selected fundamental mathematical topics 2. Collaborate with peers to solve problems that arise in mathematics and other contexts 3. Create and use representations to organize, record, and communicate mathematical ideas 4. Reflect on the process of problem solving 5. Justify results using mathematical reasoning 6. Communicate mathematical thinking clearly to peers and to the instructor The learning objectives and course content align with on?campus versions of this type of course. We are building this MOOC around key concepts and skills in the nationally recognized Common Core State Standards for Mathematics, the ACT College Readiness Standards, and the SAT Skills Insight. Students successfully completing our MOOC will find their subject matter knowledge to be in alignment with the "typical" course offered by other U.S. colleges and universities. By using Common Core standards, ACT College Readiness Standards, and the SAT Skills Insight, we can also begin to develop post?test instruments that will assess the students' levels of proficiency

This graduate level course is more extensive and theoretical treatment of the material in Computability, and Complexity (6.045J / 18.400J). Topics include Automata and Language Theory, Computability Theory, and Complexity Theory.

This course is an elementary introduction to number theory with no algebraic prerequisites. Topics covered include primes, congruences, quadratic reciprocity, diophantine equations, irrational numbers, continued fractions, and partitions. 

This course covers topics such as sums of independent random variables, central limit phenomena, infinitely divisible laws, Levy processes, Brownian motion, conditioning, and martingales.

The course consists of a sampling of topics from algebraic combinatorics. The topics include the matrix-tree theorem and other applications of linear algebra, applications of commutative and exterior algebra to counting faces of simplicial complexes, and applications of algebra to tilings.

The main aims of this seminar will be to go over the classification of surfaces (Enriques-Castelnuovo for characteristic zero, Bombieri-Mumford for characteristic p), while working out plenty of examples, and treating their geometry and arithmetic as far as possible.