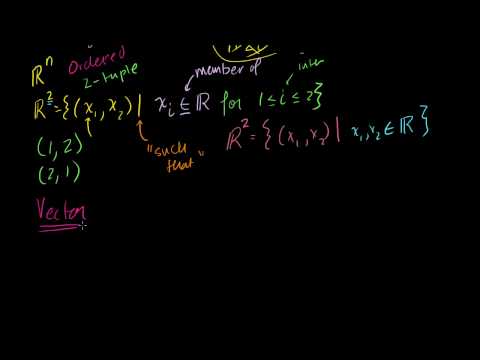Courses tagged with "Class2Go" (384)

Khan Academy at Eastside College Prep. Khan Academy in Los Altos School District. Khan Academy at Summit Prep. Khan Academy at KIPP. Khan Academy at Oakland Unity High School. Khan Academy at Marlborough School. 60 minutes: Khan Academy in the classroom. NPR Story on KA Los Altos Pilots (June 2011). The Gates Notes: Administrators in Los Altos. The Gates Notes: Teachers in Los Altos. The Gates Notes: Students in Los Altos. The Gates Notes: Insights into students' progress. Khan Academy at Eastside College Prep. Khan Academy in Los Altos School District. Khan Academy at Summit Prep. Khan Academy at KIPP. Khan Academy at Oakland Unity High School. Khan Academy at Marlborough School. 60 minutes: Khan Academy in the classroom. NPR Story on KA Los Altos Pilots (June 2011). The Gates Notes: Administrators in Los Altos. The Gates Notes: Teachers in Los Altos. The Gates Notes: Students in Los Altos. The Gates Notes: Insights into students' progress.

LeBron James asks questions about math and science, and we answer!. LeBron Asks: What muscles do we use when shooting a basket?. LeBron Asks: How does shooting a basketball illustrate Newton's 3rd Law?. LeBron Asks: If Earth's history were a basketball game, when did humans appear?. LeBron Asks: Why does sweating cool you down?. LeBron Asks: Why does humidity make it feel hotter?. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Monte Carlo Simulation to Answer LeBron's Question. LeBron Asks: What muscles do we use when shooting a basket?. LeBron Asks: How does shooting a basketball illustrate Newton's 3rd Law?. LeBron Asks: If Earth's history were a basketball game, when did humans appear?. LeBron Asks: Why does sweating cool you down?. LeBron Asks: Why does humidity make it feel hotter?. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Monte Carlo Simulation to Answer LeBron's Question.

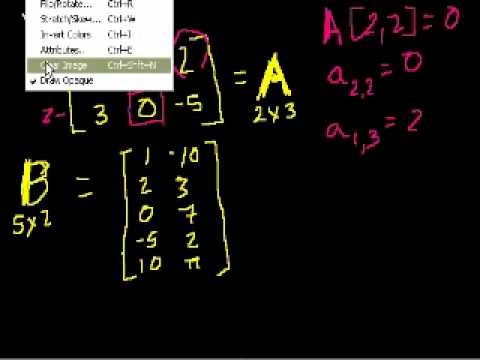
Matrices, vectors, vector spaces, transformations. Covers all topics in a first year college linear algebra course. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra. Introduction to matrices. Matrix multiplication (part 1). Matrix multiplication (part 2). Idea Behind Inverting a 2x2 Matrix. Inverting matrices (part 2). Inverting Matrices (part 3). Matrices to solve a system of equations. Matrices to solve a vector combination problem. Singular Matrices. 3-variable linear equations (part 1). Solving 3 Equations with 3 Unknowns. Introduction to Vectors. Vector Examples. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Orthogonal Complements. Rank(A) = Rank(transpose of A). dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Showing that A-transpose x A is invertible. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes.

We explore creating and moving between various coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems. Orthogonal Complements. dim(V) + dim(orthogonal complement of V)=n. Representing vectors in Rn using subspace members. Orthogonal Complement of the Orthogonal Complement. Orthogonal Complement of the Nullspace. Unique rowspace solution to Ax=b. Rowspace Solution to Ax=b example. Projections onto Subspaces. Visualizing a projection onto a plane. A Projection onto a Subspace is a Linear Transforma. Subspace Projection Matrix Example. Another Example of a Projection Matrix. Projection is closest vector in subspace. Least Squares Approximation. Least Squares Examples. Another Least Squares Example. Coordinates with Respect to a Basis. Change of Basis Matrix. Invertible Change of Basis Matrix. Transformation Matrix with Respect to a Basis. Alternate Basis Transformation Matrix Example. Alternate Basis Transformation Matrix Example Part 2. Changing coordinate systems to help find a transformation matrix. Introduction to Orthonormal Bases. Coordinates with respect to orthonormal bases. Projections onto subspaces with orthonormal bases. Finding projection onto subspace with orthonormal basis example. Example using orthogonal change-of-basis matrix to find transformation matrix. Orthogonal matrices preserve angles and lengths. The Gram-Schmidt Process. Gram-Schmidt Process Example. Gram-Schmidt example with 3 basis vectors. Introduction to Eigenvalues and Eigenvectors. Proof of formula for determining Eigenvalues. Example solving for the eigenvalues of a 2x2 matrix. Finding Eigenvectors and Eigenspaces example. Eigenvalues of a 3x3 matrix. Eigenvectors and Eigenspaces for a 3x3 matrix. Showing that an eigenbasis makes for good coordinate systems.

Understanding how we can map one set of vectors to another set. Matrices used to define linear transformations. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible. A more formal understanding of functions. Vector Transformations. Linear Transformations. Matrix Vector Products as Linear Transformations. Linear Transformations as Matrix Vector Products. Image of a subset under a transformation. im(T): Image of a Transformation. Preimage of a set. Preimage and Kernel Example. Sums and Scalar Multiples of Linear Transformations. More on Matrix Addition and Scalar Multiplication. Linear Transformation Examples: Scaling and Reflections. Linear Transformation Examples: Rotations in R2. Rotation in R3 around the X-axis. Unit Vectors. Introduction to Projections. Expressing a Projection on to a line as a Matrix Vector prod. Compositions of Linear Transformations 1. Compositions of Linear Transformations 2. Matrix Product Examples. Matrix Product Associativity. Distributive Property of Matrix Products. Introduction to the inverse of a function. Proof: Invertibility implies a unique solution to f(x)=y. Surjective (onto) and Injective (one-to-one) functions. Relating invertibility to being onto and one-to-one. Determining whether a transformation is onto. Exploring the solution set of Ax=b. Matrix condition for one-to-one trans. Simplifying conditions for invertibility. Showing that Inverses are Linear. Deriving a method for determining inverses. Example of Finding Matrix Inverse. Formula for 2x2 inverse. 3x3 Determinant. nxn Determinant. Determinants along other rows/cols. Rule of Sarrus of Determinants. Determinant when row multiplied by scalar. (correction) scalar multiplication of row. Determinant when row is added. Duplicate Row Determinant. Determinant after row operations. Upper Triangular Determinant. Simpler 4x4 determinant. Determinant and area of a parallelogram. Determinant as Scaling Factor. Transpose of a Matrix. Determinant of Transpose. Transpose of a Matrix Product. Transposes of sums and inverses. Transpose of a Vector. Rowspace and Left Nullspace. Visualizations of Left Nullspace and Rowspace. Rank(A) = Rank(transpose of A). Showing that A-transpose x A is invertible.

Let's get our feet wet by thinking in terms of vectors and spaces. Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A). Introduction to Vectors. Vector Examples. Scaling vectors. Adding vectors. Parametric Representations of Lines. Linear Combinations and Span. Introduction to Linear Independence. More on linear independence. Span and Linear Independence Example. Linear Subspaces. Basis of a Subspace. Vector Dot Product and Vector Length. Proving Vector Dot Product Properties. Proof of the Cauchy-Schwarz Inequality. Vector Triangle Inequality. Defining the angle between vectors. Defining a plane in R3 with a point and normal vector. Cross Product Introduction. Proof: Relationship between cross product and sin of angle. Dot and Cross Product Comparison/Intuition. Vector Triple Product Expansion (very optional). Normal vector from plane equation. Point distance to plane. Distance Between Planes. Matrices: Reduced Row Echelon Form 1. Matrices: Reduced Row Echelon Form 2. Matrices: Reduced Row Echelon Form 3. Matrix Vector Products. Introduction to the Null Space of a Matrix. Null Space 2: Calculating the null space of a matrix. Null Space 3: Relation to Linear Independence. Column Space of a Matrix. Null Space and Column Space Basis. Visualizing a Column Space as a Plane in R3. Proof: Any subspace basis has same number of elements. Dimension of the Null Space or Nullity. Dimension of the Column Space or Rank. Showing relation between basis cols and pivot cols. Showing that the candidate basis does span C(A).

Topics covered in a traditional college level introductory macroeconomics course. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Moderate Inflation in a Good Economy. Stagflation. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve. Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates. The Business Cycle. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Breakdown of Gas Prices. Short-Run Oil Prices. Keynesian Economics. Risks of Keynesian Thinking. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis.

Topics covered in a traditional college level introductory macroeconomics course. Introduction to Economics. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Moderate Inflation in a Good Economy. Stagflation. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve. Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates. The Business Cycle. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Breakdown of Gas Prices. Short-Run Oil Prices. Keynesian Economics. Risks of Keynesian Thinking. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis.

Aggregate demand and aggregate supply. Keynesian thinking. Demand-pull and cost-push inflation. Fiscal and monetary policy. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. The Business Cycle. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Keynesian Economics. Risks of Keynesian Thinking. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. The Business Cycle. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Keynesian Economics. Risks of Keynesian Thinking.

Aggregate demand and aggregate supply. Keynesian thinking. Demand-pull and cost-push inflation. Fiscal and monetary policy. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. The Business Cycle. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Keynesian Economics. Risks of Keynesian Thinking. Aggregate Demand. Shifts in Aggregate Demand. Long-Run Aggregate Supply. Short Run Aggregate Supply. Demand-Pull Inflation under Johnson. Real GDP driving Price. Cost Push Inflation. The Business Cycle. Monetary and Fiscal Policy. Tax Lever of Fiscal Policy. Keynesian Economics. Risks of Keynesian Thinking.

Balance of payments. Current account. Capital account. Currency reserves and speculative attacks. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis.

Balance of payments. Current account. Capital account. Currency reserves and speculative attacks. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis. Balance of Payments- Current Account. Balance of Payments- Capital Account. Why Current and Capital Accounts Net Out. Accumulating Foreign Currency Reserves. Using Reserves to Stabilize Currency. Speculative Attack on a Currency. Financial Crisis in Thailand Caused by Speculative Attack. Math Mechanics of Thai Banking Crisis.

Circular flow of income and expenditure. Gross domestic product. Introduction to Economics. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator. Introduction to Economics. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator.

Circular flow of income and expenditure. Gross domestic product. Introduction to Economics. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator. Introduction to Economics. Circular Flow of Income and Expenditures. Parsing Gross Domestic Product. More on Final and Intermediate GDP Contributions. Investment and Consumption. Income and Expenditure Views of GDP. Components of GDP. Examples of Accounting for GDP. Real GDP and Nominal GDP. GDP Deflator. Example Calculating Real GDP with a Deflator.

Consumption function. Marginal propensity to consume and multiplier. Keynesian Cross and IS-LM model. MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model. MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model.

Consumption function. Marginal propensity to consume and multiplier. Keynesian Cross and IS-LM model. MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model. MPC and Multiplier. Mathy Version of MPC and Multiplier (optional). Consumption Function Basics. Generalized Linear Consumption Function. Consumption Function with Income Dependent Taxes. Keynesian Cross. Details on Shifting Aggregate Planned Expenditures. Keynesian Cross and the Multiplier. Investment and Real Interest Rates. Connecting the Keynesian Cross to the IS-Curve. Loanable Funds Interpretation of IS Curve. LM part of the IS-LM model. Government Spending and the IS-LM model.

Inflation and deflation. CPI-U. Real and nominal return. Phillips Curve. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Moderate Inflation in a Good Economy. Stagflation. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Moderate Inflation in a Good Economy. Stagflation. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve.

Inflation and deflation. CPI-U. Real and nominal return. Phillips Curve. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Moderate Inflation in a Good Economy. Stagflation. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve. Introduction to Inflation. Actual CPI-U Basket of Goods. Inflation Data. Real and Nominal Return. Calculating Real Return in Last Year Dollars. Relation Between Nominal and Real Returns and Inflation. Deflation. Velocity of Money Rather than Quantity Driving Prices. Deflation Despite Increases in Money Supply. Moderate Inflation in a Good Economy. Stagflation. Deflationary Spiral. Hyperinflation. Unemployment Rate Primer. Phillips Curve.

Fractional reserve banking and the money supply. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates.

Fractional reserve banking and the money supply. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates. Overview of Fractional Reserve Banking. Weaknesses of Fractional Reserve Lending. Full Reserve Banking. Money Supply- M0 M1 and M2. Simple Fractional Reserve Accounting part 1. Simple Fractional Reserve Accounting (part 2). Interest as Rent for Money. Money Supply and Demand Impacting Interest Rates.