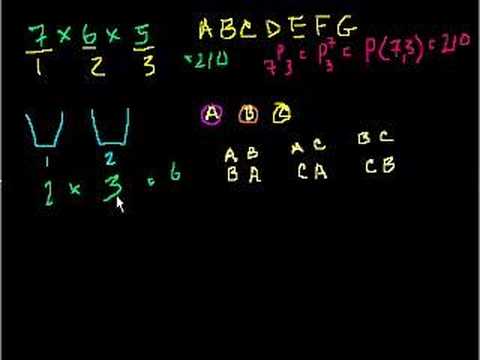Courses tagged with "Heredity and genetics" (6)

Measures of central tendency and dispersion. Mean, median, mode, variance, and standard deviation. Statistics intro: mean, median and mode. Example: Finding mean, median and mode. Mean median and mode. Exploring Mean and Median Module. Exploring mean and median. Average word problems. Sample mean versus population mean.. Reading Box-and-Whisker Plots. Constructing a box-and-whisker plot. Box-and-Whisker Plots. Creating box and whisker plots. Example: Range and mid-range. Range, Variance and Standard Deviation as Measures of Dispersion. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Unbiased Estimate of Population Variance. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Will it converge towards -1?. Variance. Population standard deviation. Sample standard deviation and bias. Statistics: Standard Deviation. Exploring Standard Deviation 1 Module. Exploring standard deviation 1. Standard deviation. Statistics: Alternate Variance Formulas. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance. Statistics intro: mean, median and mode. Example: Finding mean, median and mode. Mean median and mode. Exploring Mean and Median Module. Exploring mean and median. Average word problems. Sample mean versus population mean.. Reading Box-and-Whisker Plots. Constructing a box-and-whisker plot. Box-and-Whisker Plots. Creating box and whisker plots. Example: Range and mid-range. Range, Variance and Standard Deviation as Measures of Dispersion. Variance of a population. Sample variance. Review and intuition why we divide by n-1 for the unbiased sample variance. Simulation showing bias in sample variance. Unbiased Estimate of Population Variance. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Simulation providing evidence that (n-1) gives us unbiased estimate. Will it converge towards -1?. Variance. Population standard deviation. Sample standard deviation and bias. Statistics: Standard Deviation. Exploring Standard Deviation 1 Module. Exploring standard deviation 1. Standard deviation. Statistics: Alternate Variance Formulas. Statistics: The Average. Statistics: Variance of a Population. Statistics: Sample Variance.

Introduction to probability. Independent and dependent events. Compound events. Mutual exclusive events. Addition rule for probability. Basic Probability. Probability space exercise example. Probability space. Example: Marbles from a bag. Example: Picking a non-blue marble. Example: Picking a yellow marble. Probability 1. Probability with Playing Cards and Venn Diagrams. Addition Rule for Probability. Compound Probability of Independent Events. Getting At Least One Heads. Example: Probability of rolling doubles. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Frequency Probability and Unfair Coins. Example: Getting two questions right on an exam. Example: Rolling even three times. Independent probability. Frequency Stability. Introduction to dependent probability. Example: Dependent probability. Example: Is an event independent or dependent?. Example: Bag of unfair coins. Dependent probability. Monty Hall Problem. Intersection and union of sets. Relative complement or difference between sets. Universal set and absolute complement. Subset, strict subset, and superset. Bringing the set operations together. Basic set notation. Probability (part 1). Probability (part 2). Probability (part 3). Probability (part 4). Probability (part 5). Probability (part 6). Probability (part 7). Probability (part 8). Introduction to Random Variables. Basic Probability. Probability space exercise example. Probability space. Example: Marbles from a bag. Example: Picking a non-blue marble. Example: Picking a yellow marble. Probability 1. Probability with Playing Cards and Venn Diagrams. Addition Rule for Probability. Compound Probability of Independent Events. Getting At Least One Heads. Example: Probability of rolling doubles. LeBron Asks: What are the chances of making 10 free throws in a row?. LeBron Asks: What are the chances of three free throws versus one three pointer?. Frequency Probability and Unfair Coins. Example: Getting two questions right on an exam. Example: Rolling even three times. Independent probability. Frequency Stability. Introduction to dependent probability. Example: Dependent probability. Example: Is an event independent or dependent?. Example: Bag of unfair coins. Dependent probability. Monty Hall Problem. Intersection and union of sets. Relative complement or difference between sets. Universal set and absolute complement. Subset, strict subset, and superset. Bringing the set operations together. Basic set notation. Probability (part 1). Probability (part 2). Probability (part 3). Probability (part 4). Probability (part 5). Probability (part 6). Probability (part 7). Probability (part 8). Introduction to Random Variables.

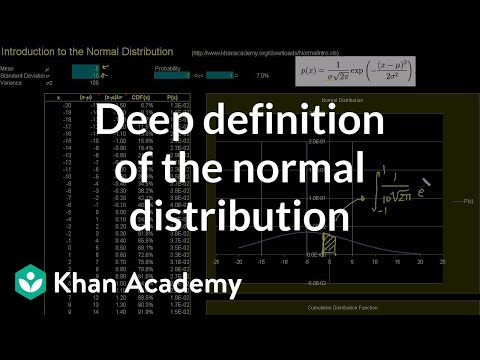
Making inferences based on sample data. Confidence intervals. Margin of error. Hypothesis testing. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. Empirical rule. ck12.org: More Empirical Rule and Z-score practice. Z scores 1. Z scores 2. Z scores 3. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Small Sample Size Confidence Intervals. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Type 1 Errors. Z-statistics vs. T-statistics. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic. Introduction to the Normal Distribution. Normal Distribution Excel Exercise. ck12.org Normal Distribution Problems: Qualitative sense of normal distributions. ck12.org Normal Distribution Problems: Empirical Rule. ck12.org Normal Distribution Problems: z-score. ck12.org Exercise: Standard Normal Distribution and the Empirical Rule. Empirical rule. ck12.org: More Empirical Rule and Z-score practice. Z scores 1. Z scores 2. Z scores 3. Central Limit Theorem. Sampling Distribution of the Sample Mean. Sampling Distribution of the Sample Mean 2. Standard Error of the Mean. Sampling Distribution Example Problem. Confidence Interval 1. Confidence Interval Example. Small Sample Size Confidence Intervals. Mean and Variance of Bernoulli Distribution Example. Bernoulli Distribution Mean and Variance Formulas. Margin of Error 1. Margin of Error 2. Hypothesis Testing and P-values. One-Tailed and Two-Tailed Tests. Type 1 Errors. Z-statistics vs. T-statistics. Small Sample Hypothesis Test. T-Statistic Confidence Interval. Large Sample Proportion Hypothesis Testing. Variance of Differences of Random Variables. Difference of Sample Means Distribution. Confidence Interval of Difference of Means. Clarification of Confidence Interval of Difference of Means. Hypothesis Test for Difference of Means. Comparing Population Proportions 1. Comparing Population Proportions 2. Hypothesis Test Comparing Population Proportions. Chi-Square Distribution Introduction. Pearson's Chi Square Test (Goodness of Fit). Contingency Table Chi-Square Test. ANOVA 1 - Calculating SST (Total Sum of Squares). ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi. ANOVA 3 -Hypothesis Test with F-Statistic.

Permutations and combinations. Using combinatorics to solve questions in probability. Permutations. Combinations. Counting 2. Example: Ways to arrange colors. Example: 9 card hands. Example: Ways to pick officers. Permutations. Combinations. Permutations and combinations. Example: Probability through counting outcomes. Example: All the ways you can flip a coin. Getting Exactly Two Heads (Combinatorics). Probability and Combinations (part 2). Probability using Combinations. Exactly Three Heads in Five Flips. Example: Different ways to pick officers. Example: Combinatorics and probability. Example: Lottery probability. Mega Millions Jackpot Probability. Generalizing with Binomial Coefficients (bit advanced). Conditional Probability and Combinations. Conditional Probability (Bayes Theorem) Visualized. Birthday Probability Problem. Probability with permutations and combinations. Permutations. Combinations. Counting 2. Example: Ways to arrange colors. Example: 9 card hands. Example: Ways to pick officers. Permutations. Combinations. Permutations and combinations. Example: Probability through counting outcomes. Example: All the ways you can flip a coin. Getting Exactly Two Heads (Combinatorics). Probability and Combinations (part 2). Probability using Combinations. Exactly Three Heads in Five Flips. Example: Different ways to pick officers. Example: Combinatorics and probability. Example: Lottery probability. Mega Millions Jackpot Probability. Generalizing with Binomial Coefficients (bit advanced). Conditional Probability and Combinations. Conditional Probability (Bayes Theorem) Visualized. Birthday Probability Problem. Probability with permutations and combinations.

Random variables. Expected value. Probability distributions (both discrete and continuous). Binomial distribution. Poisson processes. Random Variables. Discrete and continuous random variables. Probability Density Functions. Expected Value: E(X). Expected value. Law of Large Numbers. Term Life Insurance and Death Probability. Binomial Distribution 1. Binomial Distribution 2. Binomial Distribution 3. Binomial Distribution 4. Expected Value of Binomial Distribution. Galton Board Exploration. Poisson Process 1. Poisson Process 2. Random Variables. Discrete and continuous random variables. Probability Density Functions. Expected Value: E(X). Expected value. Law of Large Numbers. Term Life Insurance and Death Probability. Binomial Distribution 1. Binomial Distribution 2. Binomial Distribution 3. Binomial Distribution 4. Expected Value of Binomial Distribution. Galton Board Exploration. Poisson Process 1. Poisson Process 2.

Fitting a line to points. Linear regression. R-squared. Correlation and Causality. Fitting a Line to Data. Estimating the line of best fit exercise. Estimating the line of best fit. Squared Error of Regression Line. Proof (Part 1) Minimizing Squared Error to Regression Line. Proof Part 2 Minimizing Squared Error to Line. Proof (Part 3) Minimizing Squared Error to Regression Line. Proof (Part 4) Minimizing Squared Error to Regression Line. Regression Line Example. Second Regression Example. R-Squared or Coefficient of Determination. Calculating R-Squared. Covariance and the Regression Line. Correlation and Causality. Fitting a Line to Data. Estimating the line of best fit exercise. Estimating the line of best fit. Squared Error of Regression Line. Proof (Part 1) Minimizing Squared Error to Regression Line. Proof Part 2 Minimizing Squared Error to Line. Proof (Part 3) Minimizing Squared Error to Regression Line. Proof (Part 4) Minimizing Squared Error to Regression Line. Regression Line Example. Second Regression Example. R-Squared or Coefficient of Determination. Calculating R-Squared. Covariance and the Regression Line.